Intégrales Définies dans Matlab
Au cours de cette leçon, nous allons explorer comment effectuer le calcul d'une intégrale définie d'une fonction mathématique au sein de Matlab.
Mais d'abord, qu'entend-on exactement par intégrale définie ? Il s'agit d'un outil mathématique permettant de déterminer l'aire délimitée par une fonction f(x) - que l'on nomme aussi fonction intégrande - et l'axe des abscisses x, et ce, pour un intervalle donné [a, b]. Cette opération est symbolisée par la notation $$ \int_a^b f(x) \ dx $$
Au sein de Matlab, deux fonctions principales permettent de résoudre des intégrales définies : la première est int().
La fonction int()
Pour estimer l'intégrale définie d'une fonction sous Matlab, la fonction int() est idéalement adaptée.
int(fonction, a, b)
Elle se compose de trois paramètres :
- Le premier concerne l'expression de la fonction intégrande f(x).
- Le deuxième détermine la borne inférieure de l'intégration, soit a.
- Le troisième désigne la borne supérieure de l'intégration, soit b.
Il est essentiel de rappeler que la fonction int() opère sur la base d'un calcul symbolique. Ainsi, avant toute chose, la variable inconnue doit être définie comme un symbole via la fonction syms.
Prenons un exemple concret pour éclaircir ce point.
Considérons l'intégrale élémentaire suivante :
$$ \int_1^2 2x \ dx $$
Ici, la fonction intégrande est f(x)=2x et l'intervalle d'intégration est [1,2].
Il convient d'abord de définir x comme symbole via la fonction syms.
syms x
Puis, utilisez la commande int() en spécifiant 2*x comme premier paramètre.
Saisissez ensuite 1 comme borne inférieure et 2 comme borne supérieure de l'intervalle d'intégration [1,2].
int(2*x,1,2)
Le résultat, soit l'intégrale définie de 2x sur l'intervalle [1,2], est :
ans = 3
Dans cet exemple précis, l'intégrale définie est de 3.
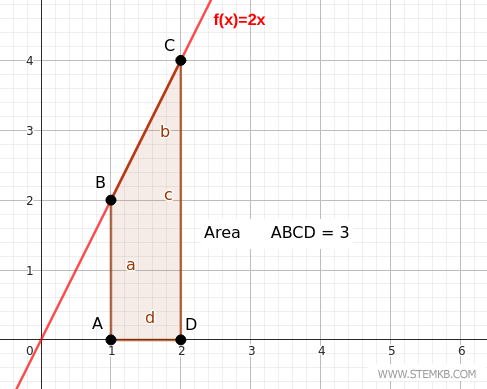
Pour confirmer ce résultat, notons que l'intégrale définie de 2x sur l'intervalle [1,2] s'évalue aisément. L'antidérivée de la fonction f(x)=2x est $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$ Une observation sur un repère cartésien nous montre que le résultat de l'intégrale définie ∫12 2x dx correspond à l'aire entre la courbe représentant f(x)=2x et l'axe des abscisses x pour l'intervalle [1,2].
La fonction quad()
Désormais, abordons la fonction quad().
Sachez qu'il est également possible de déterminer l'intégrale définie d'une fonction grâce à quad() sous Matlab. La démarche est assez directe.
Il suffit d'invoquer la fonction quad(), en spécifiant la fonction intégrande ainsi que les bornes d'intégration a et b.
quad(fonction, a, b)
Reprenons l'intégrale évoquée précédemment : de 1 à 2 pour 2x dx.
$$ \int_1^2 2x \ dx $$
La fonction intégrande est f(x)=2x avec un intervalle d'intégration [1,2].
Pour évaluer cette intégrale, définissons une fonction anonyme : f = @(x) 2*x
>> f = @(x) 2*x
Utilisez ensuite quad(f,1,2) pour estimer l'intégrale sur l'intervalle [1,2].
>> quad(f,1,2)
La fonction quad() évalue l'aire sous la courbe de la fonction f(x)=2x dans l'intervalle [1,2], et renvoie le résultat qui, dans ce cas, est 3.
ans=3
Ceci corrobore le résultat précédemment obtenu, où nous avons résolu l'intégrale analytiquement à l'aide du théorème fondamental de l'analyse. $$ \int_1^2 2x \ dx = [ x^2]_1^2 = 2^2 - 1^2 = 4 - 1 = 3 $$
Quelle est la distinction entre int et quad ?
Vous vous interrogez peut-être sur la nuance entre les fonctions int() et quad() au sein de Matlab.
En réalité, bien que ces deux fonctions soient conçues pour déterminer l'intégrale définie d'une fonction sous Matlab, elles s'appuient sur des méthodes distinctes.
- La fonction `int()` est basée sur des méthodes de résolution numérique, comme la méthode des trapèzes.
- Quant à `quad()`, elle emploie une méthode de quadrature adaptative fondée sur l'algorithme de Gauss-Kronrod. Cette dernière s'avère généralement plus efficace car nécessitant moins d'appels à la fonction à intégrer par rapport à d'autres méthodes numériques.
Voilà un tour d'horizon des méthodes d'intégration sous Matlab, un outil essentiel pour les ingénieurs, physiciens et mathématiciens.
Avec un peu d'assiduité, vous maîtriserez sans peine quad() ainsi que les autres méthodes d'intégration numérique pour résoudre une multitude de problématiques.