Les polynômes dans Matlab

Abordons les polynômes dans Matlab.

Qu'est-ce qu'un polynôme ? Les polynômes sont simplement des expressions qui consistent en des constantes et des variables, ou monômes, avec des exposants entiers qui sont combinés en utilisant les opérations arithmétiques de base (addition, soustraction, multiplication et division). Par exemple, ceci est un polynôme de degré quatre. $$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$ Le degré du polynôme est l'exposant le plus élevé de la variable inconnue x.

Comment définir un polynôme dans Matlab

Maintenant, pour définir un polynôme dans Matlab, considérons cet exemple.

$$ P(x) = x^4 + 2x^3 - x^2 + 4x +1 $$

Le polynôme n'a qu'une seule variable inconnue (x).

Pour l'utiliser dans Matlab, vous devez définir un vecteur contenant les coefficients numériques des termes.

>> P = [1 2 -1 4 1]

La variable P est un tableau avec les coefficients numériques du polynôme P(x)=x⁴+2x³-x²+4x+1.

• Le premier élément du tableau est le coefficient 1 de x⁴
• Le deuxième élément du tableau est le coefficient 2 de 2x³
• Le troisième élément du tableau est le coefficient -1 de -x²
• Le quatrième élément du tableau est le coefficient 4 de 4x
• Le cinquième élément du tableau est le coefficient 1 de +1

Une fois créé, vous pouvez l'utiliser pour calculer les valeurs du polynôme P(x) en faisant varier la variable x à l'aide de la fonction polyval().

Par exemple, pour calculer la valeur du polynôme P(x) lorsque x=0, tapez polyval(P,0)

>> polyval(P,0)

Matlab substitue la valeur zéro à la variable inconnue x et retourne le résultat.

Dans ce cas, le résultat est 1

ans = 1

Vérification. Vous pouvez rapidement vérifier en substituant x=0 dans le polynôme $$ P(0) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(0) = (0)^4 + 2 \cdot (0)^3 - (0)^2 + 4 \cdot 0 +1 $$ $$ P(0)=1 $$ Le résultat est 1.

De même, vous pouvez calculer la valeur du polynôme P(x) lorsque x=1 en tapant polyval(P,1)

>> polyval(P,1)

Dans ce cas, le résultat est 7

ans = 7

Vérification. Pour vérifier le résultat, substituez x=1 dans le polynôme $$ P(1) = x^4 + 2x^3 - x^2 + 4x +1 $$ $$ P(1) = (1)^4 + 2 \cdot (1)^3 - (1)^2 + 4 \cdot 1 +1 $$ $$ P(1)=7 $$

Matlab offre également d'autres fonctions liées aux polynômes, comme la dérivation, l'intégration, et la recherche de racines, rendant ainsi l'analyse de polynômes simple et efficace.

Si vous le souhaitez, vous pouvez également calculer la valeur du polynôme sur une plage de valeurs de x.

Par exemple, tapez x=0:5 pour créer un tableau x avec les valeurs de 0 à 5.

>> x=0:5
x =
0 1 2 3 4 5

Calculez maintenant les valeurs du polynôme dans l'intervalle de 0 à 5 en utilisant la fonction polyval(P,x)

>> polyval(P,x)

La fonction calcule les valeurs du polynôme pour chaque élément du tableau x.

Dans ce cas, le résultat est un tableau composé de 6 éléments.

ans =
1 7 37 139 385 871

Chaque élément correspond à la valeur du polynôme dans l'intervalle (0,5).

Remarque. Le premier élément du tableau est P(0)=1 lorsque x=0. Le deuxième élément est P(1)=7 lorsque x=1. Le troisième élément est P(2)=37. Le quatrième élément est P(3)=139. Et ainsi de suite.

L'utilisation de tableaux vous permet d'effectuer rapidement tout calcul.

De plus, ils permettent également de représenter graphiquement le polynôme dans un plan cartésien en utilisant la fonction plot().

Par exemple, tapez ces commandes à la suite.

>> x=0:5;
>> P = [1 2 -1 4 1] ;
>> y=polyval(P,x);
>> plot(x,y);

Le résultat est le graphique du polynôme dans l'intervalle (0,5).

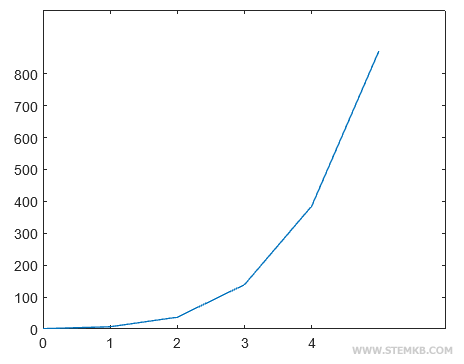
Sur l'axe horizontal sont mesurées les valeurs de la variable inconnue x, tandis que sur l'axe vertical sont indiquées celles du polynôme y.

Opérations sur les polynômes

Vous pouvez utiliser Matlab pour effectuer des opérations avec des polynômes.

Permettez-moi de vous donner un exemple pratique.

Définissez le polynôme x³+2x²+3 dans le tableau P1

>> P1 = [ 1 2 0 3 ]

Ensuite, définissez le polynôme 2x³-x²+3x+1 dans le tableau P2

>> P2 = [ 2 -1 3 1 ]

Maintenant, réalisez ces opérations :

Addition

Pour additionner les deux polynômes, tapez P1+P2

>> P1+P2
ans =
3 1 3 4

Le résultat est le polynôme 3x³+x²+3x+4

$$ P_1(x) + P_2(x) = (x^3+2x^2+3) + (2x^3-x^2+3x+1) $$ $$ P_1(x) + P_2(x) = x^3+ 2x^3+2x^2-x^2+3x+1+3 $$ $$ P_1(x) + P_2(x) = 3x^3+x^2+3x+4 $$

Soustraction

Pour calculer la différence entre les polynômes, tapez P1-P2

>> P1-P2
ans =
-1 3 -3 2

Le résultat est le polynôme -x³+3x²-3x+2

$$ P_1(x) - P_2(x) = (x^3+2x^2+3) - (2x^3-x^2+3x+1) $$ $$ P_1(x) - P_2(x) = x^3- 2x^3+2x^2+x^2-3x+1-3 $$ $$ P_1(x) + P_2(x) = -x^3+3x^2-3x-2 $$

Multiplication

Pour calculer le produit des polynômes P1·P2, il faut utiliser la fonction de convolution conv()

>> >> conv(P1,P2)
ans =
2 3 1 13 -1 9 3

Le résultat est le polynôme 2x⁶+3x⁵+x⁴+13x³-x²+9x+3

$$ P_1(x) \cdot P_2(x) = (x^3+2x^2+3) \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = x^3 \cdot (2x^3-x^2+3x+1) + 2x^2 \cdot (2x^3-x^2+3x+1) + \\ \ \ + 3 \cdot (2x^3-x^2+3x+1) $$ $$ P_1(x) \cdot P_2(x) = 2x^6-x^5+3x^4+x^3 + 4x^5-2x^4+6x^3+2x^2 + \\ \ \ + 6x^3-3x^2+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+(4x^5-x^5)+(3x^4-2x^4)+(x^3 +6x^3+ 6x^3) + \\ \ \ + (2x^2-3x^2)+9x+3 $$ $$ P_1(x) \cdot P_2(x) = 2x^6+3x^5+x^4+13x^3 -x^2+9x+3 $$

Division

Pour calculer le quotient de deux polynômes, il faut utiliser la fonction de déconvolution deconv()

>> [q,r] = deconv(P1,P2)
q = 0,50000
r = 0,00000 2,50000 -1,50000 2,50000

La fonction deconv() renvoie deux résultats :

• le polynôme quotient (q)
• le polynôme reste (r)

Le résultat est le polynôme quotient q=0,5

$$ Q = \frac{1}{2} $$

avec un reste r=2,5x²-1,5x+2,5

$$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$

Vérification. Procédez à des calculs algébriques pour vérifier si le produit est correct. $$ P_1(x) : P_2(x) = \frac{x^3+2x^2+3}{2x^3-x^2+3x+1} $$ Dans ce cas, le calcul est un peu long.

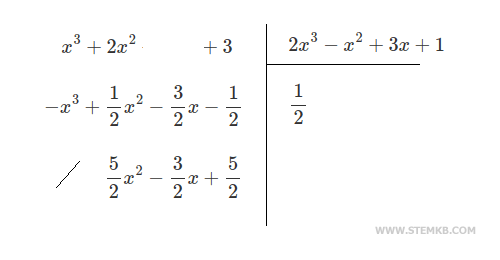
Le polynôme quotient est $$ Q= \frac{1}{2} $$ avec reste $$ R = \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ Multipliez le quotient par le polynôme diviseur et ajoutez le reste : $$ Q \cdot (2x^3 -x^2+3x+1) + R $$ $$ \frac{1}{2} \cdot (2x^3 -x^2+3x+1) + \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 - \frac{1}{2} x^2+ \frac{3}{2}x+ \frac{1}{2}+ \frac{5}{2} x^2 - \frac{3}{2} x + \frac{5}{2} $$ $$ x^3 + \frac{5-1}{2} x^2+ \frac{3-3}{2}x+ \frac{5+1}{2} $$ $$ x^3 + \frac{4}{2} x^2+ \frac{0}{2}x+ \frac{6}{2} $$ $$ x^3 + 2 x^2+ 3 $$ Le résultat est le polynôme dividende. Par conséquent, le résultat de la division entre les deux polynômes est correct.