Les Matrices sous Matlab
Dans cette session pratique, nous allons explorer comment définir une matrice avec Matlab. Vous verrez qu'il est possible de créer des matrices tant carrées que rectangulaires.
Je vous propose de voir cela à travers un exemple concret.
Commencez par créer une matrice carrée 2x2, comportant deux lignes et deux colonnes.
$$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$
Pour définir cette matrice sous Matlab, initialisez une variable de type tableau et insérez les éléments de la matrice entre crochets, en les séparant par des espaces. Ainsi, pour m = [1 2 3 4].
Il vous faudra ensuite séparer les lignes de la matrice à l'aide de points-virgules (;).
Saisissez m = [ 1 2 ; 3 4 ]
>> m = [ 1 2 ; 3 4 ]
Note. Il est possible de séparer les éléments d'une ligne par des espaces (m=[1 2;3 4]) ou des virgules (m=[1,2;3,4]), le résultat restera identique. Il est cependant recommandé d'utiliser des espaces pour une meilleure visibilité des points-virgules séparant les lignes. L'utilisation de virgules peut parfois réduire la lisibilité, surtout si les éléments de la matrice sont des nombres décimaux.
Matlab va alors définir un tableau de deux lignes et deux colonnes avec les éléments spécifiés.
Vous obtiendrez ainsi une matrice carrée 2x2.
m =
1 2
3 4
Une fois la matrice créée, vous pouvez utiliser cette variable tableau dans diverses opérations de calcul matriciel.
Exemple. Par exemple, sous Matlab, vous pouvez calculer le déterminant de la matrice, son rang, la somme ou le produit de deux matrices, ainsi que l'inverse ou la transposition d'une matrice. Pour calculer le déterminant de la matrice m, il suffit de taper det(m).

Création de matrices rectangulaires sous Matlab
La procédure pour créer une matrice rectangulaire reste similaire.
Prenons pour exemple la définition d'une matrice rectangulaire de 3x4, avec trois lignes et quatre colonnes :
$$ \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{pmatrix} $$
Pour la construire dans Matlab, entrez les 12 éléments de la matrice dans une variable tableau.
Séparez les éléments par des espaces ou des virgules, puis les lignes par des points-virgules.
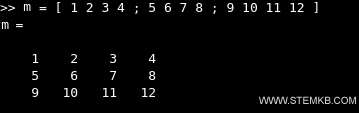
>> m = [ 1 2 3 4 ; 5 6 7 8 ; 9 10 11 12 ]
Matlab configurera alors un tableau bidimensionnel (lignes et colonnes) avec les 12 éléments arrangés en trois lignes et quatre colonnes.
Le résultat est une matrice rectangulaire 3x4.
Cette méthode vous permet de définir n'importe quelle matrice, qu'elle soit carrée ou rectangulaire, avec le nombre de lignes et de colonnes de votre choix, en deux dimensions.