Système d'équations linéaires avec Matlab

Dans cette session consacrée à Matlab, nous allons explorer comment résoudre un système d'équations linéaires en s'appuyant sur des calculs matriciels et vectoriels.

Voici un exemple concret pour illustrer notre propos.

Nous considérons ici un système d'équations linéaires à deux inconnues, structuré en deux équations.

$$ \begin{cases} x+5y-3 = 0 \\ \\ 2x-4y+8=0 \end{cases} $$

Remarque: Une équation est qualifiée de linéaire lorsque le degré le plus élevé de ses inconnues est de 1.

Reformulons ce système sous sa forme normale ax+by=c.

Transférez les termes constants à droite, en conservant les inconnues et leurs coefficients à gauche de l'équation.

$$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$

Transformons maintenant ce système en sa version vectorielle.

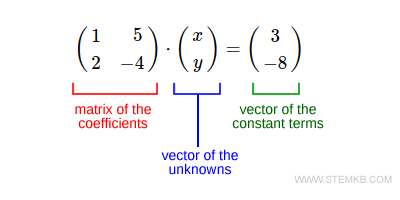
$$ \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

La matrice à gauche représente la matrice des coefficients des variables inconnues, x et y.

$$ A = \begin{pmatrix} 1 & 5 \\ 2 & -4 \end{pmatrix} $$

Le premier vecteur est celui des inconnues.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} $$

Quant au dernier vecteur, il symbolise le vecteur des termes constants des deux équations.

$$ \vec{b} = \begin{pmatrix} 3 \\ -8 \end{pmatrix} $$

Passons à présent à l'application pratique de ces concepts dans l'environnement de travail de Matlab.

Pour définir la matrice des coefficients sous Matlab, il faut créer un tableau bidimensionnel.

Entrez A = [1, 5; 2, -4] dans la ligne de commande.

>> A = [ 1 , 5 ; 2 , -4 ]
A =
1 5
2 -4

En ce qui concerne le vecteur des termes constants, créez un tableau unidimensionnel.

Entrez b = [3; -8] pour le définir.

>> b = [ 3 ; -8 ]
b =
3
-8

Le système d'équations en forme vectorielle résulte du produit d'une matrice par un vecteur.

$$ A \cdot \vec{x} = \vec{b} $$

Pour isoler les solutions du système, nous exprimons le vecteur x en isolant les autres termes sur le côté droit.

$$ \vec{x} = A^{-1} \cdot \vec{b} $$

Ici, A^-1 désigne la matrice inverse de la matrice des coefficients A du système d'équations.

Pour calculer A^-1·b dans Matlab, tapez la commande inv(A)*b.

>> inv(A)*b
ans =
-2
1

Ces calculs nous révèlent les valeurs de x et y dans le vecteur des inconnues.

$$ \vec{x} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$

Ainsi, nous obtenons la solution du système d'équations.

$$ x=-2 $$

$$ y=1 $$

Le système d'équations linéaires a donc pour solution (x;y)=(-2;1).

Vérification de la solution: Remplaçons les valeurs x=-2 et y=1 dans le système d'équations initial et effectuons les calculs algébriques. $$ \begin{cases} x+5y=3 \\ \\ 2x-4y=-8 \end{cases} $$ $$ \begin{cases} -2 + 5 \cdot 1 =3 \\ \\ 2 \cdot (-2) -4 \cdot 1 =-8 \end{cases} $$ $$ \begin{cases} 3 =3 \\ \\ -8 =-8 \end{cases} $$ Toutes les équations du système sont validées. La solution x=-2 et y=1 est donc correcte.