La fonction polyfit() sous Matlab
Laissez-moi vous présenter une fonction particulièrement astucieuse de Matlab : polyfit(). Elle est conçue pour déterminer un polynôme s'adaptant parfaitement à une série de données.
polyfit(Y)
Cette fonction utilise comme argument un tableau qui contient vos données.
Considérons, par exemple, ce jeu de données :
>> X = [ 1 2 3 4 5 6 ]
>> Y = [ 3 8 6 9 7 8 ]
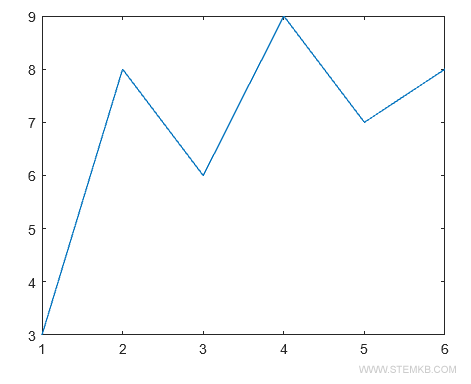
Pour représenter graphiquement cette série, la fonction plot(X,Y) est idéale.
>> plot(X,Y)
Voici le graphique obtenu :
Pour ajuster un polynôme de premier degré à ces données, il suffit d'utiliser polyfit(X,Y,1). Cette fonction retourne les coefficients du polynôme.
>> P = polyfit(X,Y,1)
Le résultat se présente ainsi :
P =
0.71429 4.33333
Ces chiffres correspondent aux coefficients du polynôme de premier degré :
$$ P_1(x) = 0.71429 \cdot x + 4.33333 $$
Pour calculer les valeurs du polynôme à chaque point du tableau X, utilisez la fonction polyval(), en lui passant les coefficients du polynôme et le tableau X.
>> polyval(P,X)
La fonction renvoie les valeurs du polynôme pour chaque élément de X :
ans =
5.0476 5.7619 6.4762 7.1905 7.9048 8.6190
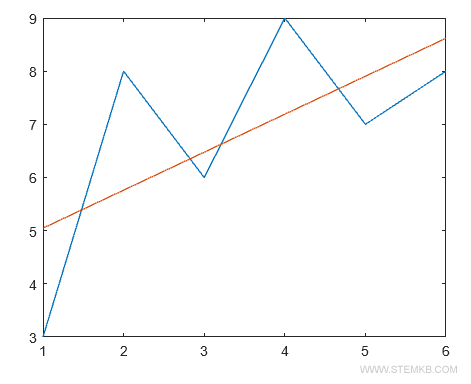
Pour visualiser les données et le polynôme sur un plan cartésien, rien de mieux que la fonction plot().
plot(X,Y,X,polyval(P,X))
Ce polynôme de premier degré (linéaire) représente une approximation linéaire de la série de données.
Exemple 2
Si maintenant votre objectif est de déterminer un polynôme de second degré pour ces données, il suffit d'utiliser polyfit() avec le paramètre 2.
>> P = polyfit(X,Y,2)
Cela vous fournit les coefficients du polynôme de second degré, à utiliser avec polyval() pour les valeurs correspondantes de chaque élément de X.
P =
-0.35714 3.21429 1.00000
Voici les coefficients obtenus pour le polynôme de second degré :
$$ P_2(x) = -0.35714 \cdot x^2 + 3.21429 \cdot x + 1.0 $$
La fonction polyval(P,X) vous permettra de calculer les valeurs du polynôme.
>> polyval(P,X)
Le résultat est un tableau des valeurs du polynôme pour chaque point de X :
ans =
3.8571 6.0000 7.4286 8.1429 8.1429 7.4286
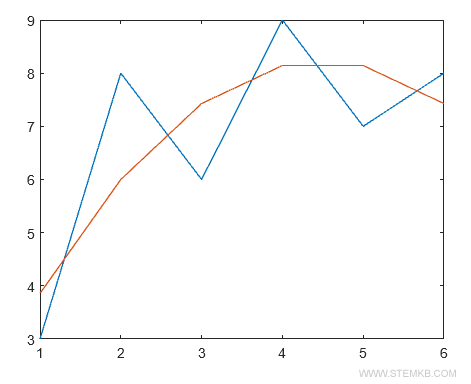
Comme précédemment, utilisez la fonction plot() pour afficher les données et le polynôme sur un plan cartésien.
plot(X,Y,X,polyval(P,X))
Le polynôme de second degré (ligne rouge) offre une meilleure approximation de la série de données.
Exemple 3
Pour finir, vous pouvez répéter le processus avec un polynôme de troisième degré.
>> P = polyfit(X,Y,3)
Voici les coefficients obtenus :
P =
0.18519 -2.30159 9.08466 -3.66667
Ces coefficients correspondent au polynôme de troisième degré.
$$ P_3(x) = 0.18519 \cdot x^3 -2.30159 \cdot x^2 + 9.08466 \cdot x - 3.66667 $$
Utilisez polyval(P,X) pour obtenir les valeurs du polynôme.
>> polyval(P,X)
La fonction fournit les valeurs du polynôme pour chaque point de X :
ans =
3.3016 6.7778 7.8730 7.6984 7.3651 7.9841
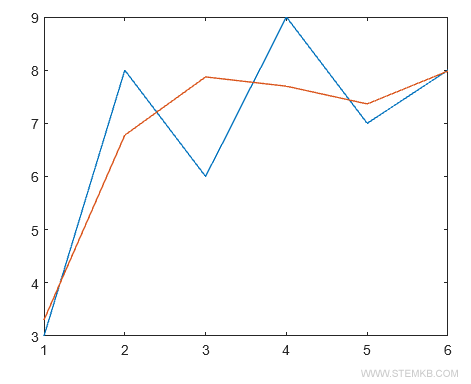
Visualisez l'ensemble sur un graphique cartésien avec la fonction plot().
plot(X,Y,X,polyval(P,X))
Le polynôme de troisième degré (ligne rouge) s'adapte encore mieux aux données.
Plus le degré du polynôme est élevé, plus l'ajustement aux données est précis. Voici donc un outil indispensable pour adapter au mieux un polynôme à vos données sous Matlab.