Les Variables Symboliques dans Matlab

Aujourd'hui, nous nous penchons sur une notion centrale de Matlab : les variables symboliques.

Mais qu'est-ce qu'une variable symbolique au juste ? Il s'agit d'une variable qui conserve uniquement un symbole, comme "x", destiné aux calculs. Elle ne retient aucune valeur numérique définie. Cette particularité offre la possibilité d'entreprendre des opérations algébriques symboliques, qu'il s'agisse de résoudre des équations avec plusieurs inconnues ou d'additionner des polynômes.

Pour initialiser une variable symbolique, la fonction syms est de mise.

Prenons un exemple simple. Si vous souhaitez définir une variable symbolique nommée "x" :

>> syms x

Il est tout aussi aisé de déclarer simultanément plusieurs variables symboliques. Il suffit de les énumérer, séparées par des espaces :

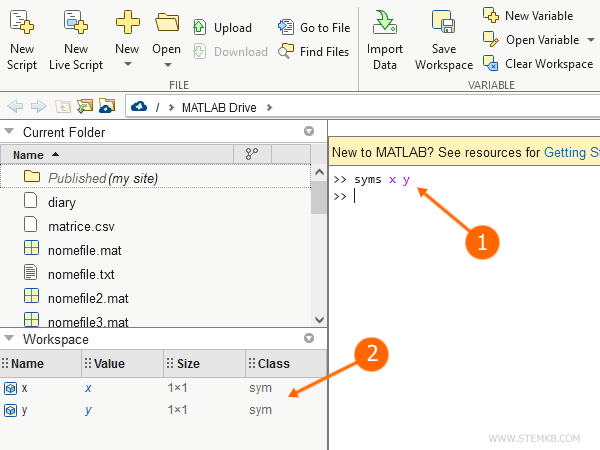
>> syms x y

Une fois déclarée, chaque variable symbolique est visible dans l'espace de travail de Matlab.

Elles appartiennent, d'ailleurs, à la classe "sym".

Plongeons dans un cas pratique.

Imaginez avoir en main deux polynômes :

$$ P(x) = 2x + y $$

$$ Q(x) = 4x - 2y $$

Votre mission ? Les multiplier.

$$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$

Pour conduire cette opération dans Matlab, initialisez d'abord les variables symboliques "x" et "y" :

>> syms x y

Ensuite, introduisez l'expression suivante :

>> pq = (2*x+y)*(4*x-2*y)

ans =
(4*x - 2*y)*(2*x + y)

Matlab, identifiant "x" et "y" comme des symboles, construit l'expression symbolique correspondante.

Contrairement à une approche numérique, Matlab traite ici "x" et "y" comme des représentations symboliques, non comme des valeurs à substituer.

Pour affiner notre calcul, faisons appel à la fonction expand(pq)

>> expand(pq)

ans =
8*x^2 - 2*y^2

Grâce à cette démarche, Matlab nous fournit le produit des polynômes sous forme d'une expression algébrique.

Le résultat est l'expression 8x²-2y²

Pour attester de la justesse du résultat, procédons à la multiplication algébrique des deux polynômes : $$ P(x) \cdot Q(x) = (2x + y) \cdot (4x - 2y) $$ $$ P(x) \cdot Q(x) =2x \cdot 4x + 2x \cdot (-2y) + y \cdot 4x + y \cdot (-2y) $$ $$ P(x) \cdot Q(x) =8x^2 - 4xy + 4xy -2y^2 $$ $$ P(x) \cdot Q(x) =8x^2 -2y^2 $$ Comme en témoignent ces opérations, notre résultat est impeccable. Voilà pour cette introduction aux variables symboliques dans Matlab.