Limite d'une fonction avec Matlab
Plongeons aujourd'hui dans l'univers captivant des limites de fonctions, en exploitant les puissantes capacités de Matlab. Notre objectif ? Non seulement assimiler le concept, mais également l'appliquer au moyen d'exemples concrets.
Mais avant de nous lancer, clarifions ce que signifie véritablement une limite de fonction. Il s'agit de la valeur vers laquelle une fonction converge lorsque sa variable indépendante approche d'un point précis. Autrement dit, elle décrit le comportement de la fonction à proximité de ce point.
Initiez cette exploration en introduisant 'x', notre variable indépendante, dans la ligne de commande Matlab, à l'aide de la commande 'syms'.
syms x
Pour démarrer, considérons la fonction f(x) = (x+1) / (x-1). Notre ambition est de déterminer la limite de 'x' tendant vers l'infini.
$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$
Il vous sera alors nécessaire d'employer la commande 'limit()'. Introduisez la fonction f(x) comme premier paramètre, 'x' en second et 'Inf' pour représenter l'infini positif en troisième. Validez ensuite par la touche entrée.
limit((x+1)/(x-1),x,Inf)
Sans attendre, Matlab calcule et affiche la limite de la fonction.
ans = (sym) 1
Il s'avère donc que la limite de notre fonction, lorsque 'x' tend vers l'infini, est unitaire.
Mais ne vous contentez pas de ma parole. Comme en témoigne le résultat, la limite de f(x) lorsque 'x' s'oriente vers l'infini positif est bien de un. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$ La limite de cette fonction atteint ainsi un lorsque 'x' s'étire vers l'infini. La conclusion est claire : lorsque x tend vers ∞, la fonction converge vers 1.
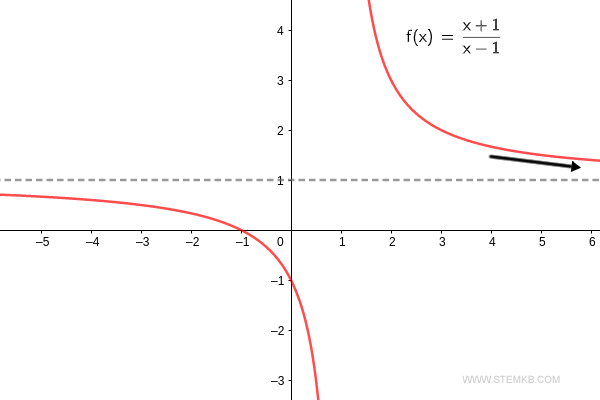
Si la limite pour x tendant vers -∞ vous intrigue, ajustez simplement le troisième paramètre en '-inf'.
limit((x+1)/(x-1),x,-inf)
Lorsque 'x' plonge abruptement vers l'infini négatif, la fonction gravite, quant à elle, vers un.
ans = (sym) 1
Pour en avoir le cœur net, constatons que la limite de f(x) pour x convergeant vers -∞ est bel et bien un. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$ Ainsi, lors de son élongation vers l'infini négatif, la fonction converge vers 1.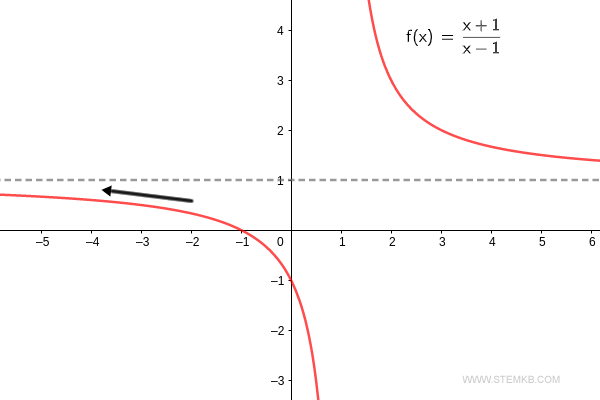
Pour examiner la limite en un point d'accumulation spécifique, tel que 'x0', substituez simplement ce point en tant que troisième paramètre.
À titre illustratif, si nous visons la limite de la fonction pour 'x' approchant de deux.
limit((x+1)/(x-1),x,2)
La limite se révèle être trois.
ans = (sym) 3
Pour validation, la limite de f(x) lorsque x converge vers 2 s'établit à trois. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$ Ainsi, lors de sa déviation vers 2, la fonction atteint une limite de 3.
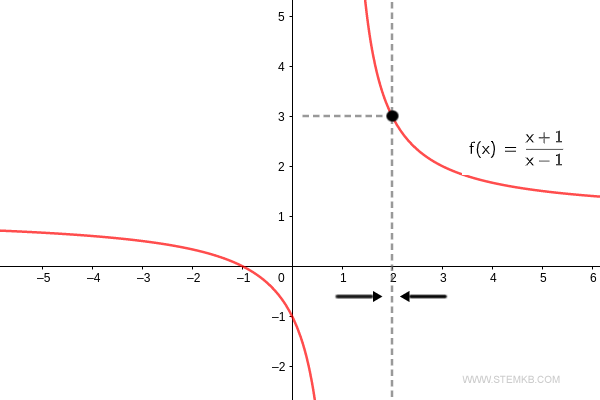
Si la limite à droite vous intéresse spécifiquement, ajoutez simplement 'right' comme quatrième argument.
limit((x+1)/(x-1),x,1,'right')
Et quel est le verdict ? La limite à droite de la fonction pour 'x' s'approchant de 1 est l'infini positif (∞).
ans = (sym) ∞
Pour en être sûr, notons que la fonction f(x) converge vers l'infini positif lorsqu'elle se rapproche de x=1 par la droite. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$ Ainsi, en se rapprochant de 1, la limite à droite de la fonction s'envole vers l'infini.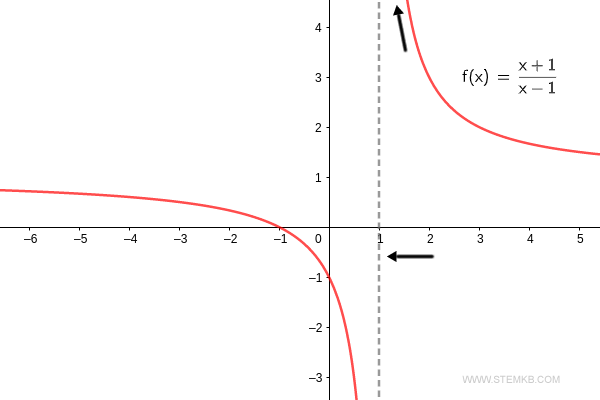
Inversement, si c'est la limite à gauche qui retient votre attention, intégrez 'left' comme quatrième paramètre.
limit((x+1)/(x-1),x,1,'left')
Le résultat ? Lorsque 'x' converge vers 1 par la gauche, la fonction décroît brutalement vers l'infini négatif (-∞).
ans = (sym) -∞
À l'observation, la fonction f(x) s'effondre bel et bien vers l'infini négatif lorsqu'elle approche de x=1 par la gauche. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$ Par conséquent, la limite à gauche de la fonction se précipite vers l'infini négatif à l'approche de l'unité.

Avec ces connaissances, vous voilà parfaitement outillé pour manipuler Matlab dans l'optique de déterminer des limites de fonctions.