Transposer une matrice dans Octave
Au cours de cette leçon, nous allons décortiquer ensemble la méthode de transposition d'une matrice sous Octave.
Premièrement, qu'est-ce que signifie transposer une matrice ? En termes simples, la transposition d'une matrice revient à transformer chaque ligne en colonne et inversement. Prenons comme exemple la matrice M, constituée de deux lignes et trois colonnes.
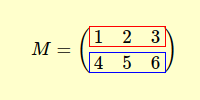
La matrice transposée MT, quant à elle, est une matrice dont les éléments de chaque ligne sont disposés en colonne.
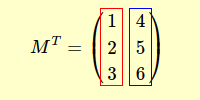
Passons maintenant à un exemple concret.
Commençons par créer une matrice rectangulaire contenant six éléments :
>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6
Comme vous pouvez le constater, notre matrice comprend deux lignes et trois colonnes.
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} $$
Pour obtenir la matrice transposée, saisissez simplement le nom de la variable suivie d'une apostrophe : M'
>> M'
ans =
1 4
2 5
3 6
Une autre manière de transposer la matrice consiste à utiliser la commande transpose(M)
>> transpose(M)
ans =
1 4
2 5
3 6
Dans les deux cas, le résultat est bel et bien la matrice transposée.
Cette matrice transposée est donc une matrice rectangulaire 3x2, où les lignes sont disposées en colonnes :
$$ M^T = \begin{pmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{pmatrix} $$
Notez bien que la première ligne de notre matrice initiale était constituée des éléments [1 2 3]. Ces mêmes éléments forment à présent la première colonne de la matrice transposée. Il en va de même pour la deuxième ligne : les éléments [4 5 6] de la matrice initiale constituent la deuxième colonne de la matrice transposée.