Matrice Creuse avec Octave

Lors de cette leçon en ligne, je vais vous montrer comment créer une matrice creuse dans Octave.

Qu'est-ce qu'une matrice creuse, me demandez-vous? À quoi sert-elle? Quand vous créez une matrice de grande taille avec beaucoup de zéros, vous occupez inutilement une grande partie de la mémoire de l'ordinateur. Par exemple, une matrice diagonale n'a que des valeurs non nulles sur la diagonale principale et des zéros partout ailleurs. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ Vous pouvez obtenir le même résultat en créant une matrice creuse où les zéros sont compressés, ce qui vous permet d'économiser de l'espace mémoire.

Les matrices creuses sont particulièrement utiles pour créer des matrices identités et des matrices diagonales compressées.

La matrice identité creuse

Pour illustrer cela, je vais vous donner un exemple pratique.

Tapez eye(4) pour créer une matrice identité:

>> eye(4)
ans =
Diagonal Matrix1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Il y a 12 zéros et 4 uns dans cette matrice. Beaucoup d'espace est donc inutilement occupé par des valeurs nulles.

Vous pouvez obtenir la même matrice identité en utilisant la technique de la matrice creuse avec la commande speye(4)

>> speye(4)
ans =
Compressed Column Sparse (rows = 4, cols = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

La matrice creuse ne stocke que les positions (ligne, colonne) où il y a des valeurs non nulles, ce qui lui permet d'occuper moins d'espace mémoire.

C'est pour cette raison qu'elle est appelée une "matrice creuse" (sparse matrix).

Remarque. Seules les informations utiles sont stockées dans la matrice creuse. Dans une matrice identité, les valeurs nulles sont sans importance. Elles sont donc éliminées. Cela réduit l'espace mémoire occupé et rend le calcul matriciel plus rapide. C'est particulièrement vrai si la matrice est très grande.

Vous pouvez utiliser la matrice creuse que vous venez de créer dans vos calculs comme si c'était une matrice identité 4x4.

Par exemple, créez une matrice avec 4 colonnes.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Maintenant, multipliez la matrice M par la matrice identité.

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Ensuite, multipliez la matrice M par la matrice identité creuse.

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Le résultat est le même.

Dans le second cas, vous avez occupé moins de mémoire et le temps de calcul est moindre.

La matrice diagonale creuse

Pour créer une matrice diagonale creuse avec des valeurs autres que 1, utilisez spdiags()

>> spdiags([1;2;3],0,3,3)
ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

• Le premier paramètre est un vecteur colonne [1; 2; 3] contenant les éléments de la diagonale.
• Le second paramètre est l'indice de la diagonale, où le nombre zéro (0) est la diagonale principale.
• Les troisième et quatrième paramètres sont le nombre de lignes (3) et de colonnes (3) de la matrice creuse.

Le résultat obtenu est la matrice creuse d'une matrice diagonale 3x3.

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Définir une matrice creuse en ne spécifiant que les valeurs non nulles

Vous pouvez également créer une matrice creuse en spécifiant uniquement les valeurs non nulles et leur position dans la matrice.

Par exemple, créez une matrice creuse avec ces valeurs:

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Définissez un tableau avec autant de lignes qu'il y a de valeurs non nulles dans le tableau.

Inscrivez le numéro de ligne, le numéro de colonne, et la valeur de l'élément non nul dans chaque ligne du tableau.

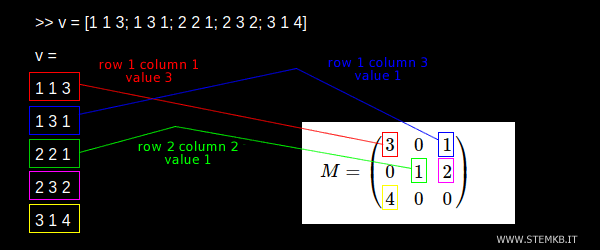
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Remarque. Le premier élément non nul (3) est dans la première ligne et la première colonne (1,1). Par conséquent, la première ligne du vecteur est 1 1 3. Le deuxième élément non nul (1) est dans la première ligne et la troisième colonne. D'où, la deuxième ligne du vecteur est 1 3 1. Le troisième élément non nul (2) est dans la deuxième ligne et la deuxième colonne. Donc, la troisième ligne du vecteur est 2 2 2. Et ainsi de suite.

Maintenant, pour créer la matrice creuse, utilisez la fonction spconvert()

>> spconvert(v)

Le résultat est une matrice creuse avec les valeurs aux positions que vous avez indiquées.

ans =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

Dans le tableau utilisé pour construire la matrice creuse, vous pouvez définir les valeurs non nulles dans l'ordre qui vous convient.

Remarque. Vous pouvez également indiquer plusieurs valeurs pour la même position dans la matrice. Lorsqu'une position dans le tableau apparaît plusieurs fois dans le tableau, Octave additionne les valeurs sans erreur. Par exemple, définissez une matrice sparse en indiquant à la position (1,1) la valeur 2 et la valeur 3. À la position (1,1) Octave ajoute les deux valeurs 2 + 3 = 5.

Avec cette méthode, vous pouvez également créer une matrice creuse avec des nombres complexes.