La rotation d'une matrice dans Octave
Dans le cadre de cette leçon, je vais vous guider à travers le processus de rotation d'une matrice dans Octave, en illustrant chaque étape avec des exemples concrets.
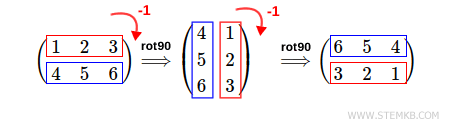
Qu'est-ce que la rotation d'une matrice ? Il s'agit d'un processus par lequel une matrice est tournée soit dans le sens horaire (vers la droite), soit dans le sens anti-horaire (vers la gauche). Pour illustrer, si vous effectuez une rotation de 90 ° dans le sens horaire sur une matrice, vous obtiendrez un résultat similaire à celui-ci :
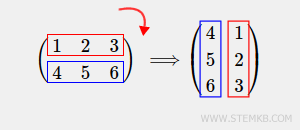
Créons d'abord une matrice rectangulaire 2x3
>> M = [ 1 2 3 ; 4 5 6 ]
M =
1 2 3
4 5 6
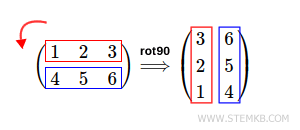
Maintenant, effectuons une rotation de 90 ° dans le sens anti-horaire sur cette matrice.
Pour cela, tapez rot90(M,1)
>> rot90(M,1)
ans =
3 6
2 5
1 4
Le résultat est une rotation à gauche de 90 ° de la matrice initiale.
Il est important de noter que vous pouvez obtenir le même résultat en tapant simplement rot90(M), car Octave définit par défaut le deuxième paramètre à 1. La direction par défaut est anti-horaire (vers la gauche), conformément aux conventions couramment adoptées en mathématiques et en physique. Pour effectuer une rotation de la matrice vers la droite, vous devez indiquer un nombre négatif, par exemple -1.
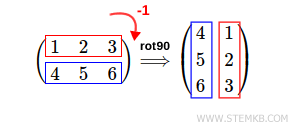
Si vous souhaitez effectuer une rotation de la matrice de 90 ° vers la droite, tapez rot90 (M, -1).
Dans ce cas, le deuxième paramètre est un entier négatif, soit -1.
>> rot90(M,-1)
ans =
4 1
5 2
6 3
Cette fois, le résultat est la matrice tournée de 90 ° vers la droite.
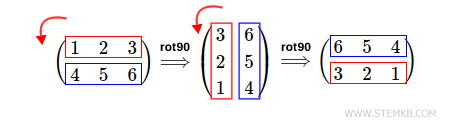
Il est également possible de faire tourner la matrice de 180 ° vers la gauche.
Pour cela, tapez rot90(M,2)
>> rot90(M,2)
ans =
6 5 4
3 2 1
Le résultat est une double rotation de 90 ° de la matrice vers la gauche.
De la même manière, vous pouvez effectuer une rotation de la matrice de 180 ° vers la droite en tapant rot90(M, -2).
Dans ce cas, le deuxième paramètre est un entier négatif, soit -2.
>> rot90(M,-2)
ans =
6 5 4
3 2 1
Le résultat est une double rotation de 90 ° de la matrice vers la droite.
Vous pouvez effectuer autant de rotations que vous le souhaitez sur la matrice en utilisant la fonction rot90(M, n).
Le deuxième paramètre indique le nombre de rotations à effectuer vers la gauche (n> 0) ou vers la droite (n <0).
Par exemple, pour effectuer une rotation de la matrice de 270 ° vers la gauche, tapez rot90(M,3)
>> rot90(M,3)
ans =
4 1
5 2
6 3
Le résultat est la matrice tournée trois fois de 90 ° vers la gauche.
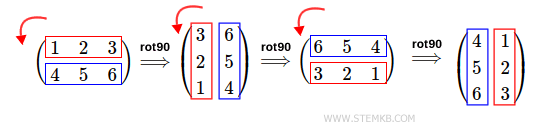
Pour effectuer une rotation dela matrice de 270 ° vers la droite, il suffit de taper rot90(M, -3), en indiquant -3 comme deuxième paramètre de la fonction.
Pour effectuer une rotation de la matrice de 360 ° vers la gauche, tapez rot90(M,4)
>> rot90(M,4)
ans =
1 2 3
4 5 6
Dans ce cas, vous obtenez la matrice initiale, car vous avez effectué quatre rotations de 90 ° vers la gauche, ce qui revient à effectuer une rotation complète.
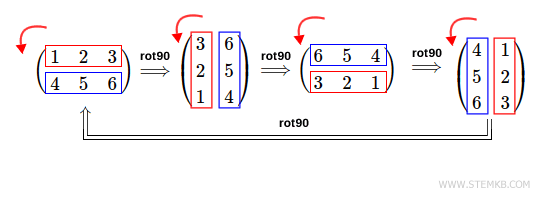
En résumé, la fonction rot90() dans Octave offre une méthode flexible et puissante pour effectuer des rotations de matrice dans le cadre de vos travaux en algèbre linéaire.