Remplacement des diagonales d'une matrice dans Octave
Dans cette leçon, nous allons explorer comment substituer les éléments d'une diagonale d'une matrice.
Qu'entend-on par diagonales d'une matrice ? Il s'agit des éléments situés sur les diagonales qui débutent en haut à droite pour finir en bas à gauche, et inversement. Par exemple, la diagonale principale de la matrice M est constituée des éléments 1, 5, 9. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
Passons à un exemple concret.
Créez une matrice 3x3
>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9
La diagonale principale est formée des éléments 1, 5, 9.
$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
Pour substituer les éléments de la diagonale principale par -1, -2, -3, saisissez spdiags([-1;-5;-9],0,M)
>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9
- Le premier paramètre est un vecteur colonne [-1;-5;-9] contenant les nouveaux éléments de la diagonale.
- Le deuxième paramètre (0) est l'indice de la diagonale. L'indice de la diagonale principale est 0.
Notez que l'indice 1 correspond à la diagonale au-dessus de la diagonale principale, tandis que l'indice -1 correspond à celle en dessous.
- Le troisième paramètre M est la variable où la matrice est stockée.
Le résultat est une matrice carrée avec les nouveaux éléments sur la diagonale principale.
$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$
Pour modifier les éléments sur la diagonale au-dessus de la diagonale principale, saisissez spdiags([-1;-5;-9],1,M)
>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9
La fonction remplace les éléments situés au-dessus de la diagonale principale.
$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$
Notez que le premier élément -1 du vecteur colonne [-1;-5;-9] n'apparaît pas dans la nouvelle matrice car, dans ce cas, il est en dehors de la matrice.
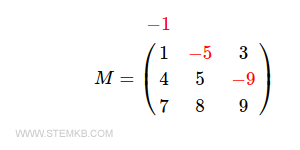
Pour remplacer les éléments sur la diagonale secondaire, il faut combiner les fonctions spdiags() et fliplr()
>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9
La fonction remplace les valeurs sur la diagonale secondaire de la matrice.
La diagonale secondaire commence en haut à droite et se termine en bas à gauche.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$
Ainsi, vous pouvez également remplacer toutes les valeurs sur les diagonales secondaires de la matrice.