Limite d'une fonction dans Octave

Pour déterminer la limite d'une fonction à l'aide d'Octave, suivez ce guide enrichi d'exemples concrets.

Prérequis. Assurez-vous d'avoir préalablement installé le logiciel GNU Octave sur votre machine, ainsi que le module Symbolic.

Commencez par définir la variable indépendante `x` de votre fonction. Pour ce faire, utilisez la commande syms

syms x

Prenons l'exemple de la fonction f(x)=(x+1)/(x-1)

Calculez maintenant la limite lorsque x tend vers l'infini x→∞ de la fonction f(x)

$$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} $$

Utilisez la commande limit()

Saisissez le nom de la fonction f(x) en premier paramètre et le nom de la variable x en second paramètre. Puis appuyez sur entrée.

limit((x+1)/(x-1),x)

Octave détermine la limite de la fonction lorsque x→∞

ans = (sym) 1

Ce qui signifie que la limite de la fonction est 1.

Vérification. La représentation graphique de la fonction est un excellent moyen de visualiser sa tendance lorsque x se rapproche de l'infini. La limite de la fonction f(x)=(x+1)/(x-1) lorsque x→∞ est 1. $$ \lim_{x \rightarrow + \infty} \frac{x+1}{x-1} = 1 $$

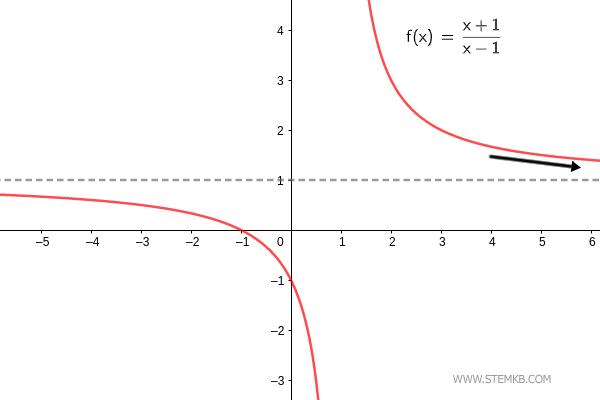
Si vous souhaitez explorer la limite de la fonction lorsque x tend vers l'opposé de l'infini, ajoutez `-inf` comme troisième argument :

limit((x+1)/(x-1),x,-inf)

Le résultat est 1.

ans = (sym) 1

Vérification. La limite de la fonction f(x)=(x+1)/(x-1) lorsque x→-∞ est 1. $$ \lim_{x \rightarrow - \infty} \frac{x+1}{x-1} = 1 $$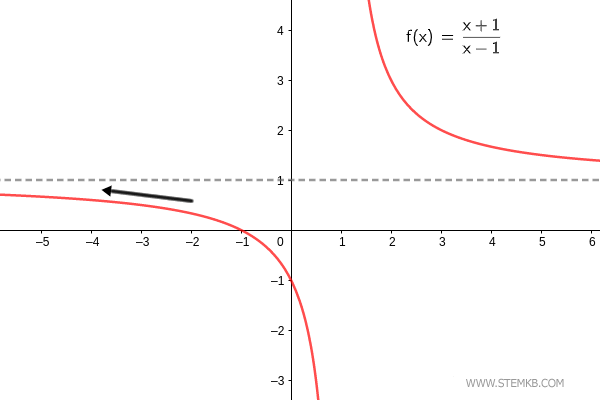

Pour évaluer en un point fini x₀, saisissez la même commande et indiquez x₀ comme troisième paramètre.

Par exemple, calculez la limite de la fonction lorsque x tend vers deux (x → 2)

limit((x+1)/(x-1),x,2)

Le résultat est 3.

ans = (sym) 3

Vérification. La limite de la fonction f(x)=(x+1)/(x-1) lorsque x→2 est 3. $$ \lim_{x \rightarrow 2} \frac{x+1}{x-1} = 3 $$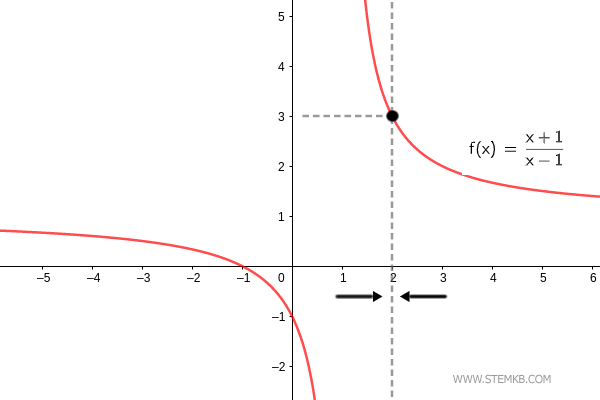

Pour des limites à droite ou à gauche, ajoutez respectivement 'right' ou 'left' comme quatrième argument.

Par exemple, pour calculer la limite à droite lorsque x tend vers deux (x → 1+)

limit((x+1)/(x-1),x,1,'right')

Le résultat est l'infini ( ∞ )

ans = (sym) ∞

Vérification. La limite à droite de la fonction f(x)=(x+1)/(x-1) lorsque x→1⁺ est infinity. $$ \lim_{x \rightarrow 1^+} \frac{x+1}{x-1} = + \infty $$

Pour calculer la limite à gauche, utilisez la même commande et saisissez 'left' comme quatrième paramètre.

limit((x+1)/(x-1),x,1,'left')

Le résultat affiché est moins l'infini ( -∞ )

ans = (sym) -∞

Vérification. La limite à droite de la fonction f(x)=(x+1)/(x-1) lorsqu x→1^- est moins l'infini. $$ \lim_{x \rightarrow 1^-} \frac{x+1}{x-1} = - \infty $$

Si ce guide vous a été bénéfique, nous vous invitons à poursuivre votre exploration d'Octave avec nous.