Extraire la diagonale d'une matrice sous Matlab
Dans ce tutoriel, je vous expliquerai comment isoler les éléments de la diagonale d'une matrice dans Matlab.
Qu'est-ce que la diagonale d'une matrice ? Il s'agit de l'ensemble des éléments alignés diagonalement, partant de l'angle supérieur gauche. Prenons un exemple : dans la matrice suivante, les éléments 1, 5 et 9, mis en évidence en rouge, forment la diagonale principale. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
Illustrons cela avec un exemple concret.
Construisez une matrice carrée de 3x3, composée de trois lignes et trois colonnes, comme suit.
>> M=[1 2 3; 4 5 6; 7 8 9]
M =
1 2 3
4 5 6
7 8 9
Utilisez ensuite la fonction diag(M) pour extraire les éléments de la diagonale principale.
>> diag(M)
ans =
1
5
9
Cette fonction sélectionne les éléments de la diagonale principale de la matrice, soit dans notre cas les valeurs 1, 5 et 9.
$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$
La fonction diag() permet également d'accéder à d'autres diagonales de la matrice.
Ainsi, en tapant diag(M,1), vous pourrez récupérer les éléments de la diagonale située juste au-dessus de la principale.
>> diag(M,1)
ans =
2
6
Dans cet exemple, diag(M,1) permet d'extraire les chiffres 2 et 6, qui se trouvent sur la diagonale immédiatement supérieure à la principale.
$$ M = \begin{pmatrix} 1 & \color{red}2 & 3 \\ 4 & 5 & \color{red}6 \\ 7 & 8 & 9 \end{pmatrix} $$
Essayez maintenant la commande diag(M,2).
>> diag(M,2)
ans = 3
Cette commande permet de sélectionner les éléments de la diagonale située encore plus haut... et ainsi de suite.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$
Pour accéder aux diagonales situées en dessous de la principale, il suffit d'utiliser un entier négatif comme second paramètre.
Par exemple, diag(M,-1) permet d'extraire les éléments de la diagonale située juste en dessous de la diagonale principale.
>> diag(M,-1)
ans =
4
8
Avec diag(M,-1), vous obtenez les éléments 4 et 8, qui se trouvent sous la diagonale principale.
$$ M = \begin{pmatrix} 1 & 2 & 3 \\ \color{red}4 & 5 & 6 \\ 7 & \color{red}8 & 9 \end{pmatrix} $$
Pour ne conserver que les éléments de la diagonale principale, en éliminant tous les autres, utilisez diag(diag(M)).
>> diag(diag(M))
ans =
Matrice Diagonale
1 0 0
0 5 0
0 0 9
Cette manipulation vous donne une matrice diagonale.
$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 9 \end{pmatrix} $$
Comment extraire la diagonale secondaire ?
La diagonale secondaire, ou antidiagonale, correspond à la diagonale allant de droite à gauche, en partant de l'élément en haut à droite. Pour notre matrice 3x3, les éléments 3, 5 et 7 en forment la diagonale secondaire.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Pour extraire cette diagonale secondaire, il faut d'abord retourner horizontalement la matrice à l'aide de la fonction fliplr().
Essayez par exemple la commande diag(fliplr(M)).
>> diag(fliplr(M))
ans =
3
5
7
Avec diag(fliplr(M)), vous accédez aux éléments de la diagonale secondaire de la matrice.
$$ M = \begin{pmatrix} 1 & 2 & \color{red}3 \\ 4 & \color{red}5 & 6 \\ \color{red}7 & 8 & 9 \end{pmatrix} $$
Note. Il est également possible d'utiliser le deuxième paramètre de la fonction pour accéder aux diagonales situées au-dessus ou en dessous de la diagonale principale. Pour extraire celles situées au-dessus de la diagonale secondaire, entrez un entier positif. Par exemple, diag(fliplr(M),1) permet d'extraire les éléments 2 et 4, situés juste au-dessus de la diagonale principale. $$ M = \begin{pmatrix} 1 & \color{red}2 & \color{green}3 \\ \color{red}4 & \color{green}5 & 6 \\ \color{green}7 & 8 & 9 \end{pmatrix} $$ Pour accéder aux diagonales en dessous de la diagonale secondaire, utilisez un entier négatif. Par exemple, diag(fliplr(M),-1) vous permet d'obtenir les éléments 6 et 8, situés en dessous de la diagonale principale.
$$ M = \begin{pmatrix} 1 & 2 & \color{green}3 \\ 4 & \color{green}5 & \color{red}6 \\ \color{green}7 & \color{red}8 & 9 \end{pmatrix} $$.
La fonction diag() permet d'extraire les éléments situés sur les diagonales, y compris dans le cas d'une matrice rectangulaire.
Imaginons, par exemple, la création d'une matrice rectangulaire de dimensions 3x4, comportant 3 rangées et 4 colonnes.
>> M2=[1 1 1 1 ; 2 2 2 2 ; 3 3 3 3]
M2 =
1 1 1 1
2 2 2 2
3 3 3 3
Il suffit ensuite de saisir la commande diag(M2).
>> diag(M2)
ans =
1
2
3
Cette commande, diag(M2), a pour effet d'extraire les éléments formant la diagonale, allant du coin supérieur gauche vers le bas à droite.
$$ M = \begin{pmatrix} \color{red}1 & 1 & 1 & 1 \\ 2 & \color{red}2 & 2 & 2 \\ 3 & 3 & \color{red}3 & 3 \end{pmatrix} $$
Cette méthode est efficace pour extraire n'importe quelle diagonale, même lorsque la matrice n'est pas carrée.
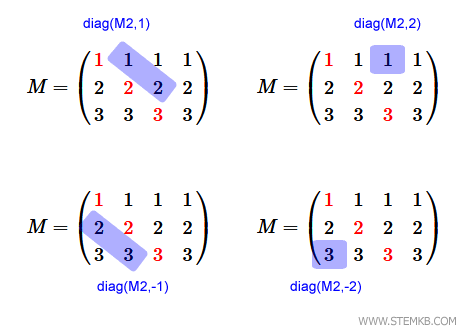
Note : Il est également possible d'extraire les diagonales situées au-dessus ou en dessous de la diagonale principale dans une matrice rectangulaire. Pour cela, indiquez un entier positif ou négatif en second paramètre. Par exemple, diag(M2,1) ou diag(M2,-1) permettent d'accéder respectivement aux diagonales supérieure et inférieure. De la même manière, diag(M2,2) ou diag(M2,-2) sont utilisés pour les diagonales suivantes.
Pour extraire les diagonales secondaires d'une matrice rectangulaire, il est nécessaire d'inverser l'ordre des colonnes de droite à gauche. Ainsi, pour obtenir la diagonale secondaire, entrez diag(fliplr(M2)). Dans ce cas, la diagonale secondaire débute à l'élément le plus en haut à droite de la matrice rectangulaire. $$ M = \begin{pmatrix} 1 & 1 & 1 & \color{red}1 \\ 2 & 2 & \color{red}2 & 2 \\ 3 & \color{red}3 & 3 & 3 \end{pmatrix} $$