Modification des diagonales dans une matrice Matlab

Dans cette leçon, je vous guiderai à travers le processus de remplacement des éléments des diagonales d'une matrice en utilisant Matlab, en illustrant les étapes de manière claire et concise.

Qu'est-ce que les diagonales d'une matrice ? Il s'agit des éléments alignés diagonalement, partant du coin supérieur droit vers le coin inférieur gauche, et vice-versa. Prenons un exemple concret : la diagonale principale de la matrice M se compose des éléments 1, 5, 9. $$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

Examinons un exemple pratique pour mieux comprendre.

Comment créer une matrice carrée 3x3 avec trois lignes et trois colonnes ? Voici comment :

>> M=[1 2 3 ; 4 5 6 ; 7 8 9]
M =
1 2 3
4 5 6
7 8 9

La diagonale principale de cette matrice est constituée des éléments 1, 5, 9.

$$ M = \begin{pmatrix} \color{red}1 & 2 & 3 \\ 4 & \color{red}5 & 6 \\ 7 & 8 & \color{red}9 \end{pmatrix} $$

En tapant spdiags([-1;-5;-9],0,M) dans la console Matlab, on remplace les éléments de la diagonale principale par -1, -5, -9.

>> spdiags([-1;-5;-9],0,M)
ans =
-1 2 3
4 -5 6
7 8 -9

• Le premier argument, le vecteur colonne [-1;-5;-9], contient les nouvelles valeurs à insérer dans la diagonale de la matrice.
• Le deuxième argument (0) indique l'indice de la diagonale concernée. L'indice 0 correspond à la diagonale principale.

  Note. L'indice 1 désigne la diagonale située au-dessus de la diagonale principale, tandis que l'indice -1 se réfère à celle située en dessous. De même, les indices 2 et -2 renvoient respectivement aux diagonales situées au-dessus et en dessous des diagonales 1 et -1.

• Le troisième argument, M, est le nom de la variable où est stockée la matrice.

Cette commande modifie la matrice en insérant de nouveaux éléments sur la diagonale principale.

$$ M = \begin{pmatrix} \color{red}{-1} & 2 & 3 \\ 4 & \color{red}{-5} & 6 \\ 7 & 8 & \color{red}{-9} \end{pmatrix} $$

Maintenant, pour modifier les éléments de la diagonale située au-dessus de la principale, utilisez la commande spdiags([-1;-5;-9],1,M).

>> spdiags([-1;-5;-9],1,M)
ans =
1 -5 3
4 5 -9
7 8 9

Cette commande remplace effectivement les éléments au-dessus de la diagonale principale de la matrice.

$$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ 4 & 5 & \color{red}{-9} \\ 7 & 8 & 9 \end{pmatrix} $$

Note. Le premier élément -1 du vecteur [-1;-5;-9] ne figure pas dans la matrice modifiée car il est en dehors des limites de celle-ci. Ainsi, seuls -5 et -9 sont visibles dans la matrice.

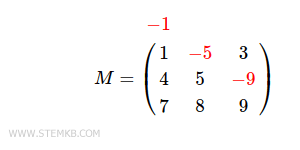
Comment remplacer les éléments de la diagonale secondaire ?

La diagonale secondaire débute en haut à droite et se termine en bas à gauche.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{3} \\ 4 & \color{red}{5} & 6 \\ \color{red}{7} & 8 & 9 \end{pmatrix} $$

Pour remplacer les éléments sur la diagonale secondaire, il est nécessaire d'utiliser conjointement les fonctions spdiags() et fliplr().

>> fliplr(spdiags([-1;-5;-9],0,fliplr(M)))
ans =
1 2 -1
4 -5 6
-9 8 9

La fonction fliplr() inverse la matrice de gauche à droite.

$$ \text{ fliplr }(M) = \begin{pmatrix} 3 & 2 & 1 \\ 6 & 5 & 4 \\ 9 & 8 & 7 \end{pmatrix} $$

Ensuite, spdiags() remplace les valeurs de la diagonale principale de cette matrice inversée.

$$ \text{ fliplr }(M) = \begin{pmatrix} \color{red}{-1} & 2 & 1 \\ 6 & \color{red}{-5} & 4 \\ 9 & 8 & \color{red}{-9} \end{pmatrix} $$

Cela entraîne le remplacement des éléments de la diagonale secondaire dans la matrice originale M.

$$ M = \begin{pmatrix} 1 & 2 & \color{red}{-1} \\ 4 & \color{red}{-5} & 6 \\ \color{red}{-9} & 8 & 9 \end{pmatrix} $$

Cette méthode permet également de modifier les valeurs sur les autres diagonales de la matrice.

Note. Pour ajuster les diagonales au-dessus ou en dessous de la diagonale secondaire, changez simplement l'indice dans la fonction spdiags() en 1 ou -1. Par exemple, pour modifier les éléments au-dessus de la diagonale secondaire, utilisez la commande
fliplr(spdiags([-1;-5;-9],1,fliplr(M))) $$ M = \begin{pmatrix} 1 & \color{red}{-5} & 3 \\ \color{red}{-9} & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} $$ Inversement, pour les éléments en dessous de la diagonale secondaire, utilisez
fliplr(spdiags([-1;-5;-9],-1,fliplr(M))) $$ M = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & \color{red}{-1} \\ 7 & \color{red}{-5} & 9 \end{pmatrix} $$