Les matrices creuses dans Matlab

Dans ce cours en ligne, je vais vous montrer comment créer efficacement des matrices creuses avec Matlab.

Qu'est-ce qu'une matrice creuse ? En bref, les matrices creuses sont une solution astucieuse pour générer des matrices de grande taille tout en minimisant l'utilisation de la mémoire informatique. Imaginez une matrice remplie de valeurs constantes, comme le zéro. Répéter ces valeurs dans de multiples éléments gaspille une quantité considérable de mémoire. $$ M = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ L'idée est de compresser ces données en ignorant les valeurs nulles, ce qui est précisément le principe des matrices creuses.

Matlab vous permet d'utiliser ces matrices pour créer des matrices d'identité et des matrices diagonales de manière compressée.

Création d'une matrice d'identité creuse

Illustrons cela par un exemple concret.

Pour créer une matrice d'identité, utilisez la fonction eye(4).

>> eye(4)
ans =
Matrice Diagonale
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1

Cette matrice contient 12 zéros et seulement 4 uns, donc la majorité de son espace (12 éléments sur 16) est occupée par des zéros superflus.

Maintenant, appliquons la méthode des matrices creuses avec la commande speye(4) pour obtenir un résultat similaire.

>> speye(4)
ans =
Matrice Creuse à Colonnes Compressées (lignes = 4, colonnes = 4, nnz = 4 [25%])
(1, 1) -> 1
(2, 2) -> 1
(3, 3) -> 1
(4, 4) -> 1

Dans cette matrice creuse, Matlab ne répertorie que les positions (ligne, colonne) ayant des valeurs non nulles, économisant ainsi de la mémoire.

Cette approche est donc nommée matrice "creuse" car elle se concentre uniquement sur l'information pertinente. Dans une matrice d'identité, les zéros sont considérés comme négligeables et sont donc omis, réduisant l'espace occupé en mémoire (complexité spatiale) et le temps de calcul (complexité temporelle).

Cette matrice creuse peut être utilisée dans vos calculs tout comme une matrice normale.

Par exemple, considérons une matrice carrée M à quatre rangées et quatre colonnes.

>> M=[1 2 3 4;5 6 7 8; 9 0 1 2; 3 4 5 6]
M =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Si nous multiplions M par une matrice d'identité de taille 4, voici le résultat :

>> M*eye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

En effectuant la même opération avec une matrice d'identité creuse de taille 4, nous obtenons :

>> M*speye(4)
ans =
1 2 3 4
5 6 7 8
9 0 1 2
3 4 5 6

Le résultat est identique, mais la version avec la matrice creuse est obtenue plus rapidement et avec moins de mémoire utilisée.

Matrices diagonales creuses

Matlab dispose également d'une fonction dédiée à la création de matrices diagonales creuses, nommée spdiags().

spdiags(v,i,r,c)

• Le premier paramètre (v) est un vecteur colonne contenant les éléments à placer sur la diagonale
• Le deuxième paramètre (i) désigne l'indice de la diagonale concernée (0 pour la diagonale principale)
• Les troisième (r) et quatrième (c) paramètres indiquent respectivement le nombre de lignes et de colonnes de la matrice creuse à générer

Par exemple, en entrant spdiags([1;2;3],0,3,3), vous créez une matrice diagonale creuse de dimensions 3x3.

>> spdiags([1;2;3],0,3,3)
ans =
Matrice Creuse à Colonnes Compressées (lignes = 3, colonnes = 3, nnz = 3 [33%])

(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3

Matlab positionne alors les éléments du vecteur [1;2;3] sur la diagonale principale, résultant en une matrice creuse.

$$ M = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \\ \end{pmatrix} $$

Comment créer manuellement une matrice creuse

Dans Matlab, il est également possible de définir une matrice creuse en listant la position de chaque valeur non nulle de la matrice.

Par exemple, pour créer une matrice creuse à partir de cette matrice

$$ M = \begin{pmatrix} 3 & 0 & 1 \\ 0 & 1 & 2 \\ 4 & 0 & 0 \end{pmatrix} $$

Rédigez la liste des valeurs non nulles de la matrice dans un tableau, en précisant la ligne, la colonne et la valeur.

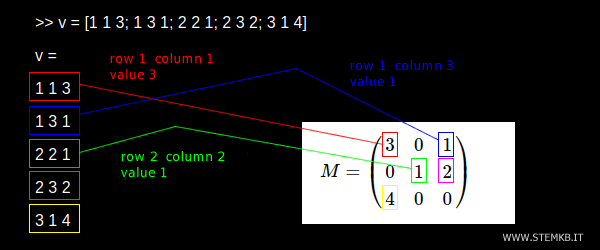
>> v = [1 1 3; 1 3 1; 2 2 1; 2 3 2; 3 1 4]
v =
1 1 3
1 3 1
2 2 1
2 3 2
3 1 4

Chaque ligne du tableau indique la position (ligne et colonne) et la valeur d'un élément non nul de la matrice.

Le premier élément non nul (3) de la matrice se trouve dans la première ligne et la première colonne (1,1). C'est l'élément écrit en rouge dans l'exemple ci-dessous. Pour indiquer cet élément dans la liste de la matrice creuse, vous devez écrire 1 1 3 dans une ligne du tableau. Et ainsi de suite.

Une fois que vous avez défini le tableau avec la liste des valeurs non nulles, créez la matrice creuse en utilisant la fonction spconvert().

>> spconvert(v)

Le résultat est une matrice creuse avec les valeurs dans les positions que vous avez indiquées.

ans =
Matrice Creuse en Colonnes Comprimées (lignes = 3, colonnes = 3, nnz = 5 [56%])
(1, 1) -> 3
(3, 1) -> 4
(2, 2) -> 1
(1, 3) -> 1
(2, 3) -> 2

Lors de la création du tableau, vous pouvez définir les éléments non nuls de la matrice dans n'importe quel ordre.

Vous pouvez également indiquer plusieurs fois la même position de la matrice en utilisant différentes valeurs.

Veuillez noter que si vous définissez plusieurs fois la même position dans la matrice dans un tableau, Matlab additionnera toutes les valeurs. Par exemple, si vous créez une matrice creuse en indiquant la valeur 2 et la valeur 3 à la position (1,1), Matlab considérera la somme des deux valeurs comme 2+3=5 à la position (1,1) dans la matrice.

Cette méthode permet également de générer une matrice creuse avec des nombres complexes.