Créer plusieurs graphiques dans Matlab
Supposons que vous ayez un ensemble de données que vous désirez explorer visuellement dans Matlab. Imaginez maintenant que vous disposiez de deux fonctions distinctes à comparer ou à analyser conjointement. Dans ce guide concis, je vais vous démontrer comment présenter ces fonctions dans un espace graphique unique, soit en les superposant (vue unique), soit en les affichant sur des graphiques distincts (vue multiple).
Il existe deux manières de créer plusieurs graphiques dans Matlab :
Vue unique avec plusieurs graphiques
Illustrons ceci par un exemple concret.
Commencez par créer un tableau de dix entiers allant de 1 à 10.
Entrez la commande x = linspace(1,10,10)
>> x = linspace(1,10,10)
x = 1 2 3 4 5 6 7 8 9 10
Ensuite, formez deux tableaux y1 et y2 correspondant à deux fonctions différentes.
$$ y1=f(x) =x^2 $$ $$ y2=g(x) =x^3 $$
La fonction y1 calcule le carré des valeurs de x, tandis que y2 évalue leur cube.
Pour générer le tableau de la fonction y1, tapez y1=x.^2.
>> y1=x.^2;
De même, créez le tableau de la fonction y2 avec y2=x.^3.
>> y2=x.^3
Les tableaux y1 et y2 sont constitués de dix nombres, reflétant les images des valeurs du tableau x.
Voici les données des tableaux x, y1 et y2 :

Pour afficher ces fonctions sur un même graphique cartésien, utilisez la commande suivante :
plot(x,y1,x,y2)
Cette approche nécessite la saisie de quatre paramètres dans la fonction plot :
- x,y1 pour tracer le graphique de y1
- x,y2 pour tracer celui de y2
Matlab génère alors un graphique multiple où deux courbes, représentant chacune une fonction, se superposent dans le même espace cartésien.
Une courbe illustre le carré de x, l'autre le cube de x.
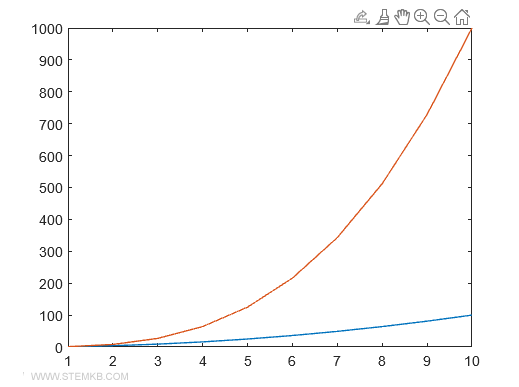
Note. De la même façon, il est possible de superposer trois fonctions ou plus sur un même graphique. Pour cela, il faudra entrer six paramètres pour trois graphiques, huit pour quatre, et ainsi de suite. Matlab différenciera automatiquement les couleurs des fonctions, mais vous pouvez aussi personnaliser ces dernières, ainsi que l'épaisseur des lignes et les symboles utilisés.
Chaque ligne du graphique se voit attribuer une couleur différente par Matlab.
Pour modifier les couleurs des lignes, utilisez les codes de couleur suivants dans l'option de couleur de la fonction plot() :
- rouge
- vert
- bleu
- cyan
- magenta
- jaune
- noir
- blanc
- aucune
Par exemple, pour obtenir une ligne rouge et une noire, entrez :
>> clf
>> hold on
>> plot(x,y1,'Color', 'red')
>> plot(x,y2,'Color', 'black')
>> hold off
L'instruction clf nettoie l'écran, tandis que hold on permet de modifier le graphique sans effacer le contenu existant.
La propriété Color permet de sélectionner et de personnaliser les couleurs des tracés.
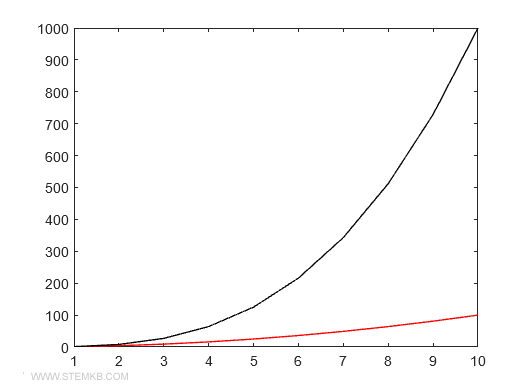
Pour ajuster l'épaisseur des lignes, utilisez la propriété Linewidth.
Exemple : pour dessiner la ligne rouge avec une plus grande épaisseur :
>> clf
>> hold on
>> plot(x,y1,'Color', 'red', 'Linewidth', 3)
>> plot(x,y2,'Color', 'black')
>> hold off
Dans ce cas, le tracé rouge ressortira davantage que le tracé noir.
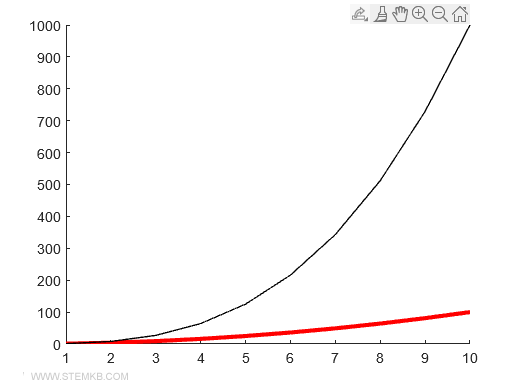
Il est également possible de varier les symboles marqueurs pour représenter les points de chaque fonction.
Les caractères x, +, -, et o sont autorisés comme marqueurs.
Par exemple, pour associer le symbole + à la première fonction et x à la seconde, procédez comme suit :
>> clf
>> hold on
>> plot(x,y1,'+','Color', 'red', 'Linewidth', 2)
>> plot(x,y2,'x','Color', 'black', 'Linewidth', 2)
>> hold off
Matlab tracera ainsi les points des deux fonctions sur le diagramme cartésien sans les relier, en utilisant les marqueurs spécifiés.
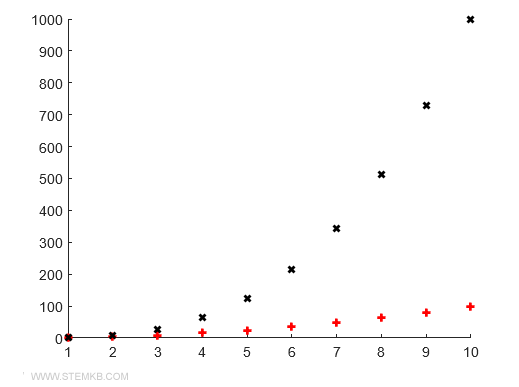
Ajout d'une légende
Pour plus de clarté, il est possible d'ajouter une légende au graphique avec la commande legend().
Indiquez les libellés de chaque tracé entre parenthèses, dans le même ordre. Par exemple :
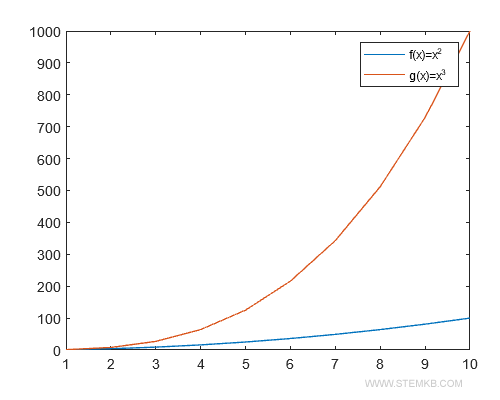
plot(x,y1,x,y2)
legend('f(x)=x^2', 'g(x)=x^3');
La légende apparaîtra alors à côté du graphique.
Vue séparée avec plusieurs graphiques
Si vous préférez présenter vos fonctions dans des graphiques distincts, adoptez la vue multiple.
Qu'est-ce qu'un graphique multiple en vue séparée ? Cela consiste à diviser votre espace graphique en sections plus petites, chacune accueillant un graphique spécifique. Cette approche permet de visualiser plusieurs fonctions de manière distincte, sans superposition.
Prenons un exemple pratique.
Créez un tableau x avec 100 éléments et deux tableaux de fonctions différents, y1 et y2.
>> x=linspace(1,100,100);
>> y1=x.^2;
>> y2=log(x);
Organisez votre espace graphique avec la commande subplot(lignes, colonnes, indice).
Les lignes et les colonnes déterminent le découpage de l'espace, tandis que l'indice spécifie la position du graphique.
Par exemple, pour deux graphiques, configurez une ligne et deux colonnes.
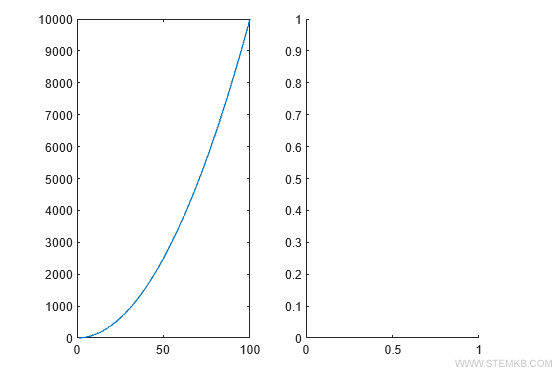
>> subplot(1,2,1)
La commande subplot(1,2,1) crée le premier diagramme cartésien dans la première ligne et colonne.
Tracez ensuite le graphique de la fonction y1 avec plot(x,y1).
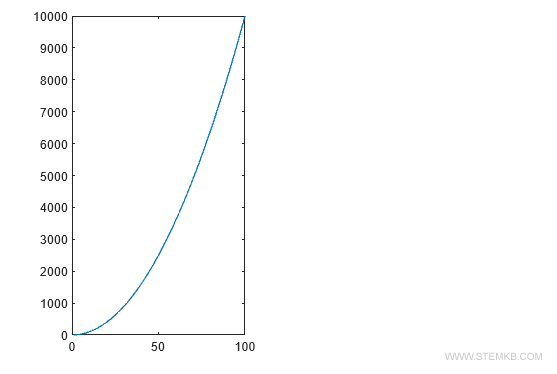
>> plot(x,y1)
Ce graphique s'affichera dans le premier diagramme de la vue multiple.
Passez ensuite au deuxième diagramme avec subplot(1,2,2).
>> subplot(1,2,2)
Cette commande ouvre un deuxième diagramme cartésien à côté du premier.
Il se situe dans la même ligne mais dans la colonne suivante.
Tracez le graphique de la fonction y2 avec plot(x,y2).
>> plot(x,y2)
Ce graphique apparaîtra dans le deuxième diagramme de la vue multiple.
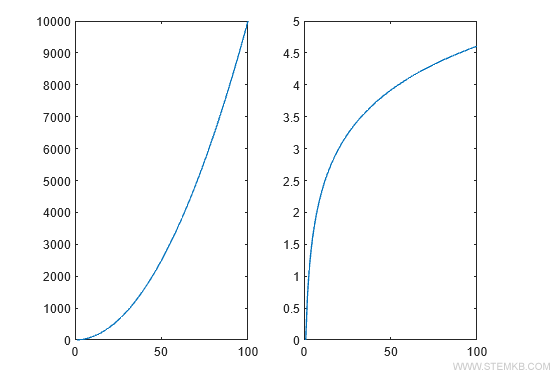
Ainsi, les deux graphiques sont présentés dans la même zone graphique, mais dans des diagrammes distincts.
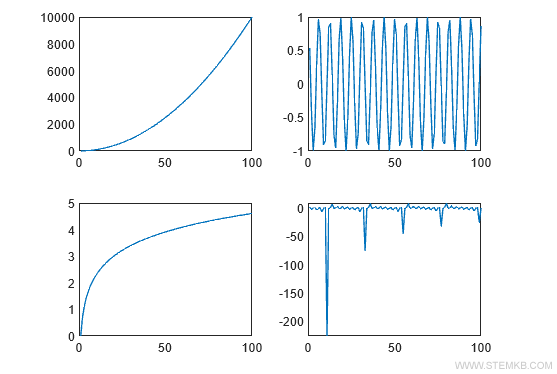
Note. Vous pouvez créer des vues multiples avec davantage de diagrammes. Par exemple, pour diviser la zone graphique en deux lignes et deux colonnes, utilisez les commandes subplot(2,2,1), subplot(2,2,2), subplot(2,2,3), subplot(2,2,4).
>> clf
>> subplot(2,2,1)
>> plot(x,y1)
>> subplot(2,2,2)
>> plot(x,y3)
>> subplot(2,2,3)
>> plot(x,y2)
>> subplot(2,2,4)
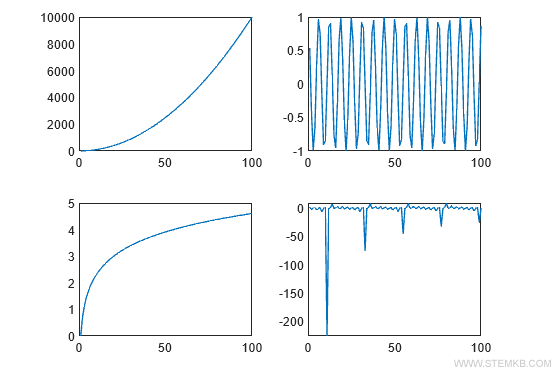
>> plot(x,y4)
Cela permet d'afficher simultanément quatre graphiques dans la même zone graphique, chacun dans un diagramme distinct, sans superposition.
Ainsi s'achève notre exploration des graphiques multiples en vue unique et séparée dans Matlab. Nous avons vu comment personnaliser les couleurs, l'épaisseur des lignes et les symboles, et comment ajouter des légendes pour enrichir nos graphiques d'informations utiles et les rendre visuellement attractifs.
En pratiquant avec Matlab, vous découvrirez qu'il offre un terrain de jeu extraordinaire pour la création et la personnalisation de graphiques.