Création de graphiques en escalier avec Matlab
Explorons aujourd'hui avec enthousiasme le monde des graphiques en escalier en utilisant Matlab !
Qu'est-ce que c'est, un graphique en escalier ? Imaginez le graphique d'une fonction, mais au lieu d'avoir un tracé fluide et continu, il présente une succession de marches d'escalier. Parfait pour illustrer de manière plus nette comment les valeurs d'une fonction augmentent ou diminuent.
Commençons par un exemple simple.
Imaginons un tableau 'x' contenant des valeurs de 1 à 20.
>> x=linspace(1,20,20);
Ce tableau 'x' servira de domaine à notre fonction.
Créons ensuite un tableau 'y' pour représenter les valeurs de notre fonction y=f(x).
>> y=x
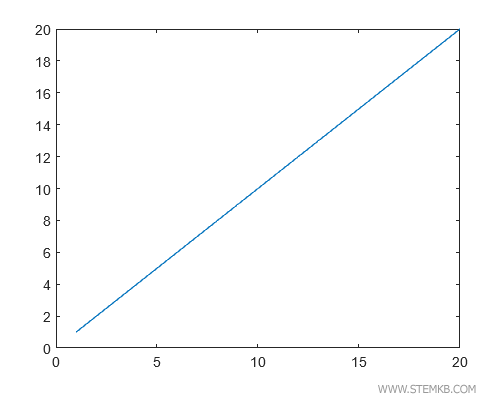
En exécutant plot(x,y), nous obtenons le graphique de y=f(x).
>> plot(x,y)
Nous observons une ligne continue allant de 1 à 20. Ici, c'est une droite qui traverse l'origine.
Intéressons-nous à quelque chose de plus captivant ! En tapant stairs(x,y), nous créons un graphique en escalier.
>> stairs(x,y)
La fonction stairs(x,y) nous permet de relier des points adjacents par des marches plutôt que par une ligne continue.
Nous obtenons ainsi un diagramme en escalier des plus astucieux.
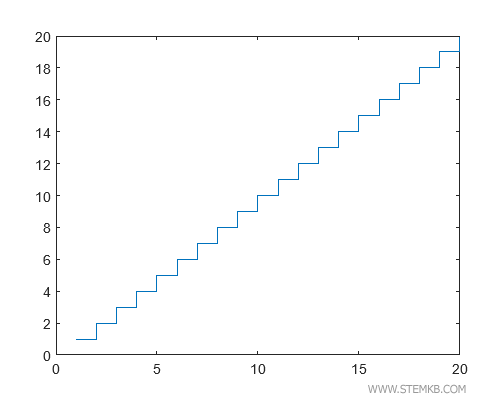
Dans cet exemple, les marches sont équivalentes, du fait de l'augmentation constante de notre fonction linéaire à chaque intervalle.
Élevons le niveau avec un exemple plus complexe.
Définissons une fonction y=x2, calculant le carré de chaque valeur de x.
y=x.^2
Le graphique continu de cette fonction nous révèle une courbe exponentielle.
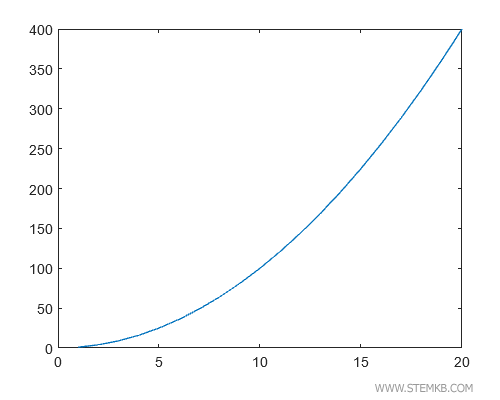
En appliquant stairs(x,y) pour créer notre diagramme en escalier...
>> stairs(x,y)
...nous obtenons un graphique composé de marches de différentes hauteurs, les plus élevées indiquant les points de croissance maximale de la fonction.
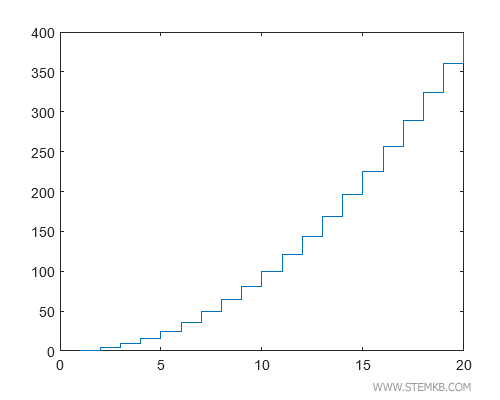
Dans ce cas, la hauteur des marches s'accroît à mesure que la valeur de x augmente, illustrant une croissance plus que proportionnelle de la fonction.
Comment afficher plusieurs graphiques en un seul diagramme ?
Vous vous demandez peut-être comment comparer deux fonctions sur le même graphique. Aucun souci !
Créons, par exemple, un tableau Y avec deux éléments.
Choisissons 0.5cos(X) comme premier élément et 2cos(X) comme second élément.
>> X = linspace(0,4*pi,50)';
>> Y = [0.5*cos(X), 2*cos(X)];
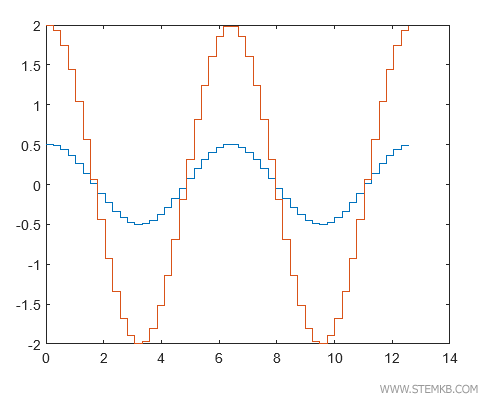
En tapant stairs(Y) ou stairs(X,Y), nous pouvons afficher ensemble les deux graphiques en escalier.
>> stairs(X,Y)
Et voilà ! Un diagramme cartésien unique qui présente les graphiques en escalier des deux fonctions, permettant une comparaison aisée de leurs comportements.

Et pour les plus ambitieux, il est même possible d'afficher trois fonctions ou plus sur le même graphique. Il suffit de définir un tableau avec autant d'éléments nécessaires et de suivre la même démarche.