Création de graphiques polaires sous Matlab

Au cours de cette leçon, je vais vous guider dans la création d'un graphique polaire sous Matlab, en abordant les étapes de manière claire et précise.

Qu'est-ce qu'un graphique polaire ? Ces graphiques séduisants se présentent sous la forme de cercles et utilisent des coordonnées polaires pour représenter les données. Appréciés pour leur élégance et leur clarté, ils sont largement utilisés dans les domaines scientifiques.

Passons à un exemple concret pour mieux comprendre.

Tout d'abord, il est nécessaire de créer un tableau nommé 'theta' pour nos variations angulaires :

>> theta = 0 : 0.1 : 2*pi;

Ce tableau, s'étendant de 0 à 2π (360 degrés), est construit avec des incréments de 0.1.

Ensuite, définissons un second tableau, 'y1', qui associe les valeurs de la fonction y1 à chaque variation angulaire dans theta :

>> y1=0.5+(1.3).^(theta);

Ainsi, 'y1' représente le codomaine de notre fonction, tandis que 'theta' s'occupe du domaine, garantissant une correspondance parfaite entre les éléments des deux tableaux.

Avec nos tableaux prêts, abordons la création du graphique polaire. Il suffit d'entrer la commande Polar() de cette manière :

 

>> PolarGraph = polar(theta,y1,"*");

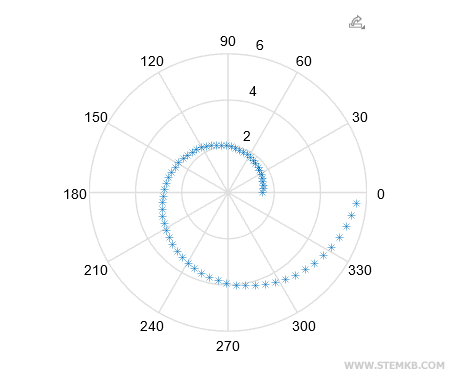
Voilà ! Matlab illustre alors avec finesse le comportement de la fonction y1 via ses coordonnées polaires.

Dans cet exemple, nous avons créé une fonction en forme de spirale fascinante.

Mais ce n'est pas tout. Comment procéder si l'on souhaite intégrer deux fonctions dans un même graphique polaire ?

Commençons par nettoyer l'écran avec 'clf' et reconstituons le tableau 'theta' avec les mêmes variations angulaires.

clf

Nous recréons ensuite le tableau 'theta' avec les mêmes variations angulaires :

>> theta = 0 : 0.1 : 2*pi;

À présent, élaborons deux tableaux, 'y1' et 'y2', chacun représentant une fonction différente évoluant avec theta :

>> y1=0.5+(1.3).^(theta);
>> y2 = 3*(1 - cos(theta));

Intégrons ces deux fonctions dans une matrice [m]

>> m = [y1;y2];

Pour finaliser, utilisons la fonction Polarplot() afin de créer le graphique polaire :

>> PolarGraph = polarplot(theta,m);

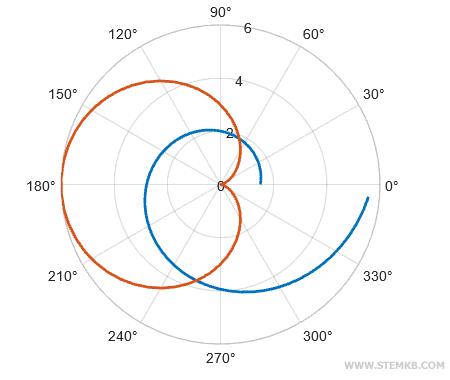
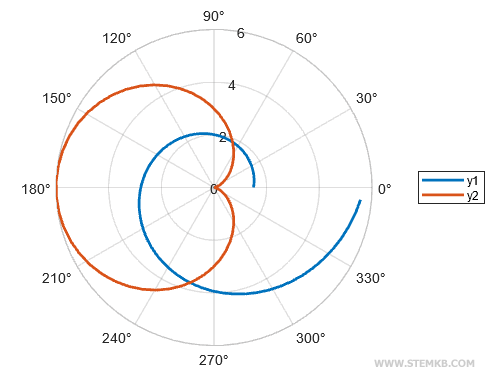
Les deux fonctions se déploient ainsi dans un seul et même graphique polaire.

Pour accentuer la visibilité des lignes du graphique, la fonction set() est de mise.

set(PolarGraph,"LineWidth",2);

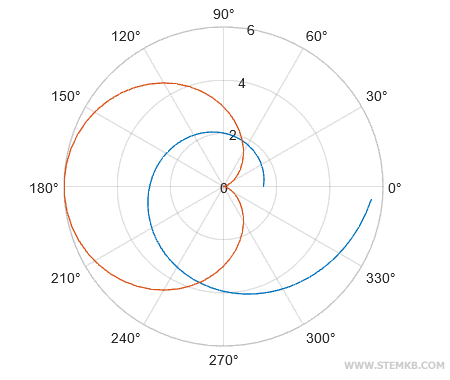
Cela permet d'augmenter l'épaisseur des lignes de manière significative.

Sublimons notre réalisation en ajoutant une légende avec la fonction legend().

legend("y1","y2");

La légende vient ainsi agrémenter avec goût notre graphique.

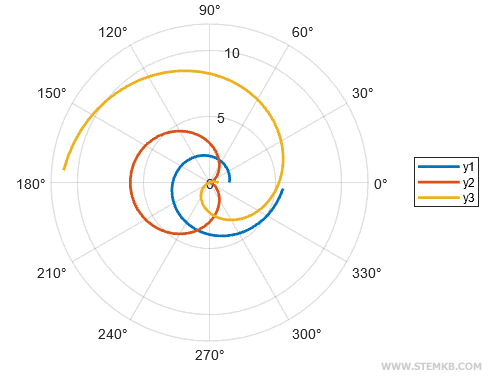
Sachez que cette méthode peut s'appliquer à plus de deux fonctions. Il est possible de représenter trois fonctions ou davantage sur un seul graphique polaire en suivant la même démarche. Définissez des fonctions supplémentaires, créez une matrice regroupant toutes les fonctions, et utilisez la fonction polarplot(theta, m) pour afficher les graphiques superposés. Le résultat est un graphique polaire captivant, mettant en scène plusieurs fonctions dans une danse visuelle. Par exemple, ajoutez une fonction y3 = 0.7 - (1.9).*theta en plus de y1 et y2. Créez ensuite une matrice contenant ces trois fonctions m = [y1; y2; y3]. Finalement, la fonction polarplot(theta, m) permet de visualiser les trois graphiques en superposition dans le même graphique polaire. Ainsi, le graphique polaire illustre trois fonctions enchevêtrées.

Le graphique polaire présente désormais trois fonctions.