Calcul de la norme d'un vecteur dans Matlab

Au cours de cette leçon, je vais vous expliquer comment calculer la norme (ou magnitude) d'un vecteur dans Matlab.

Qu'est-ce que la norme d'un vecteur ? Il s'agit de la longueur euclidienne du vecteur, également connue sous le nom de magnitude. Par exemple, la norme euclidienne d'un vecteur dans le plan correspond à la longueur de la flèche qui le représente.

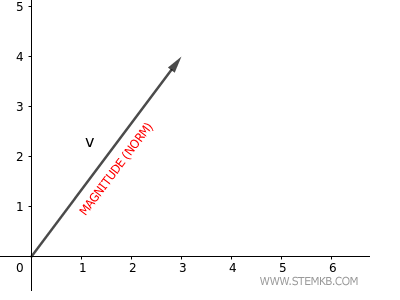
Je vais vous présenter un exemple concret.

Prenez en considération un vecteur dans la variable V.

>> V=[3 4]
V =
3 4

Ce vecteur se trouve à l'origine (0;0) du plan, son extrémité se situant au point (3;4).

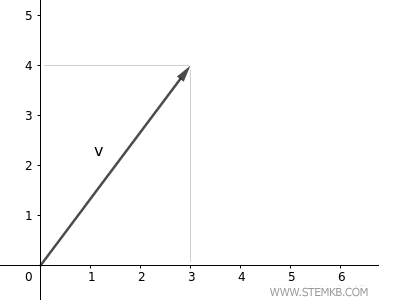
Pour calculer la longueur de ce vecteur (sa magnitude ou norme), il suffit d'utiliser la fonction norm(V).

>> norm(V)
ans = 5

La norme euclidienne de ce vecteur est donc de 5.

Cette valeur représente la longueur de la flèche symbolisant le vecteur sur le plan.

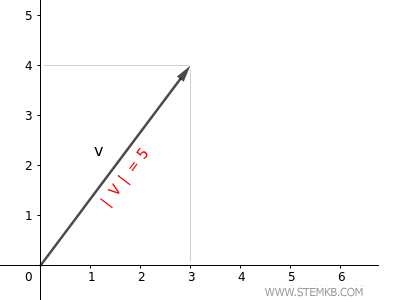
Vérification. On peut également calculer la longueur d'un vecteur en utilisant le théorème de Pythagore $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ La magnitude du vecteur est effectivement de 5, ce qui confirme l'exactitude du résultat obtenu.