Conjugaison complexe dans Octave
Dans cette leçon, je vais vous expliquer comment trouver le conjugué d'un nombre complexe dans Octave.
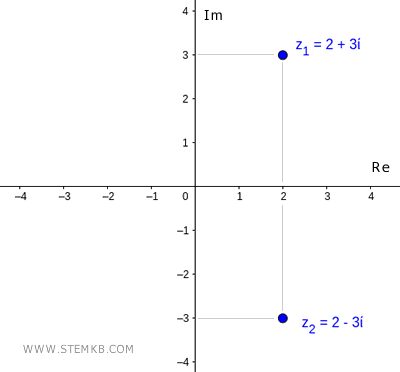
Qu'est-ce que le conjugué complexe ? Le conjugué d'un nombre complexe z = a + bi est un nombre complexe qui a la même partie réelle et la partie imaginaire avec le signe changé. Par exemple, le nombre complexe z1 = 2 + 3i a le conjugué complexe z2 = 2 - 3i, et vice versa.
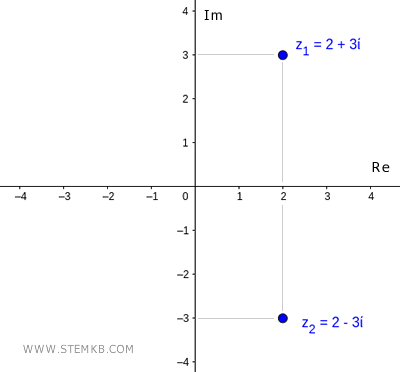
Voici un exemple pratique.
Définissez le nombre complexe z = 2 + 3i dans Octave en utilisant la fonction complex(2,3).
>> z=complex(2,3)
ans = 2 + 3i
Pour obtenir le conjugué d'un nombre complexe dans Octave, vous pouvez utiliser la fonction conj().
Par exemple, si vous avez un nombre complexe z = 2 + 3i, vous pouvez trouver son conjugué en tapant conj(z)
>> conj(z)
ans = 2 - 3i
La fonction renvoie le conjugué du nombre complexe, qui dans ce cas est 2 - 3i.
Quel est l'objectif de calculer le conjugué complexe ?
Calculer le conjugué complexe simplifie certaines opérations en arithmétique des nombres complexes.
Par exemple, le produit d'un nombre complexe avec son conjugué est égal au carré de sa magnitude.
Pour calculer cela, multipliez le nombre complexe z par son conjugué conj(z). Le produit est égal à 13.
>> z*conj(z)
ans = 13
Pour calculer le module du nombre complexe z, vous pouvez utiliser la fonction intégrée abs() dans Octave.
Le résultat de l'application de cette fonction à z est d'environ 3,6.
>> abs(z)
ans = 3.6056
En outre, calculez le carré du module de z.
Le résultat sera toujours 13.
>> (abs(z))^2
ans = 13.000
Cela implique que le module d'un nombre complexe peut également être obtenu en prenant la racine carrée du produit du nombre complexe et de son conjugué.
>> sqrt(z*conj(z))
ans = 3.6056
Si vous avez trouvé la leçon de Nigiara sur l'utilisation des nombres complexes dans Octave utile, assurez-vous de continuer à nous suivre pour en savoir plus.
Remarque. Dans le contexte des nombres complexes, "magnitude" et "module" sont souvent utilisés de manière interchangeable pour désigner la valeur absolue ou la distance d'un nombre complexe par rapport à l'origine du plan complexe.