Angle et module d'un nombre complexe dans Octave

Dans cette leçon, je vais expliquer comment calculer l'angle (argument) et le module d'un nombre complexe sur Octave.

Qu'est-ce que le module et l'angle d'un nombre complexe ? Chaque nombre complexe z=a+bi peut être représenté sur le plan complexe aux coordonnées (a,b).

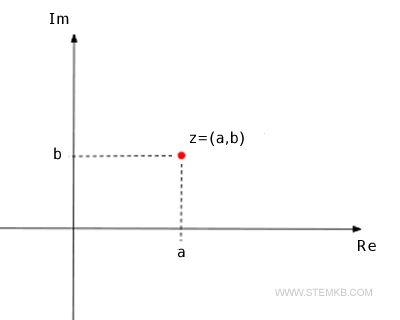
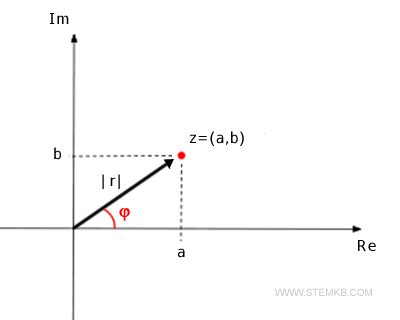
Ainsi, chaque point sur le plan est un nombre complexe différent et peut être atteint de manière unique à partir de l'origine grâce à un vecteur. La longueur r=|z| du vecteur est appelée le module du nombre complexe z. L'angle φ du vecteur mesuré dans le sens antihoraire par rapport à l'axe réel positif (Re) est appelé l'argument du nombre complexe.

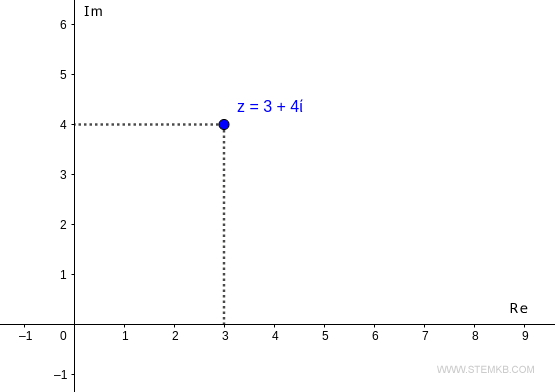
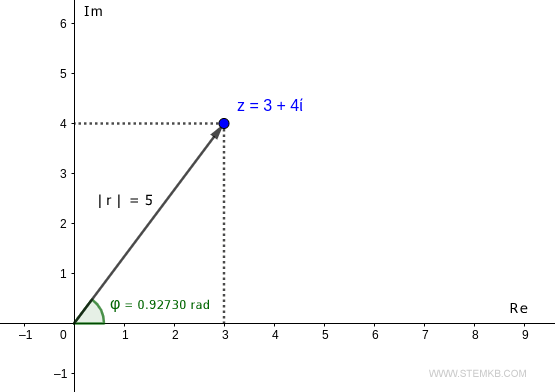
Par exemple, considérons le nombre complexe z=3+4i

Sur le plan complexe, le nombre z est situé au point de coordonnées (3,4).

Ce point est accessible depuis l'origine par un seul vecteur de longueur r et d'angle φ.

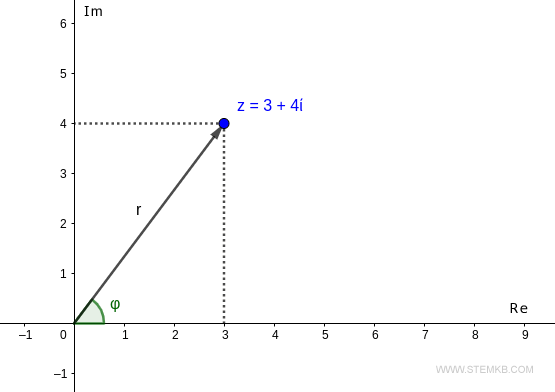
Pour calculer le module r=|z| du nombre complexe, qui est la longueur du vecteur, utilisez la fonction abs() dans Octave.

>> abs(z)
ans= 5

Par conséquent, le module du nombre complexe z=3+4i est égal à 5.

En d'autres termes, le vecteur qui relie l'origine au point (3,4) a une longueur de cinq.

Pour calculer l'angle (argument) du nombre complexe, utilisez la fonction angle() à la place.

>> angle(z)
ans = 0.92730

Octave renvoie l'angle en radians.

Dans ce cas, l'argument du nombre complexe z=3+4i est de 0,92730 radians, ce qui correspond à environ 53 degrés.

Si cette leçon sur Octave de Nigiara est utile, continuez à nous suivre.