Guide d'Octave

Dans ce guide, je vais vous présenter GNU Octave, un logiciel libre et open source similaire à Matlab, qui vous permet de résoudre des calculs mathématiques et des problèmes géométriques (tels que les matrices, l'algèbre linéaire, l'analyse mathématique, etc.).

Quels sont les avantages d'Octave?

• C'est gratuit. Vous pouvez l'installer et l'utiliser librement. Il ne nécessite aucune inscription.
• Il peut être installé sur un PC avec un système d'exploitation Windows, Linux ou Mac.
• Les commandes Octave sont très similaires à celles de Matlab. La syntaxe est presque identique.

Comment utiliser Octave?

Vous pouvez utiliser Octave de deux manières différentes

• comme une calculatrice scientifique via la ligne de commande
• comme un langage de programmation pour écrire et enregistrer des fichiers de script

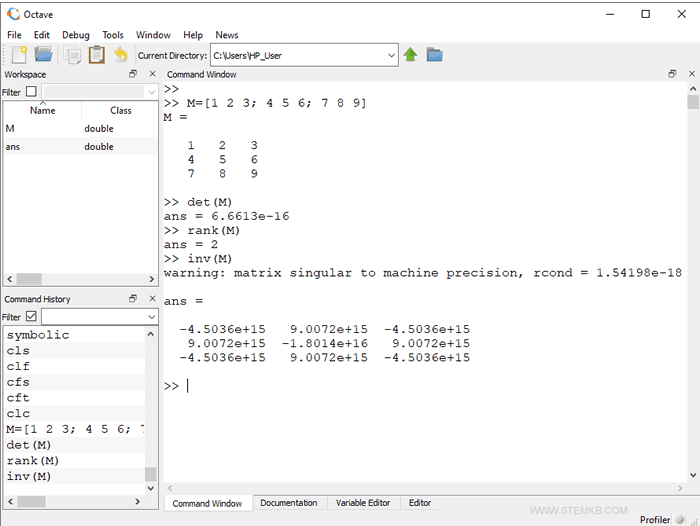
Voici l'interface graphique d'Octave

Le menu principal d'Octave (File, Edit, Debug, Window, Help, News) se trouve en haut.

Au centre de l'interface, il y a la fenêtre de commande ( command window ) qui vous permet d'utiliser Octave de manière interactive.

À gauche, il y a plusieurs panneaux :

• gestionnaire de fichiers ( file manager )
• espace de travail ( workspace )
• commandes historiques

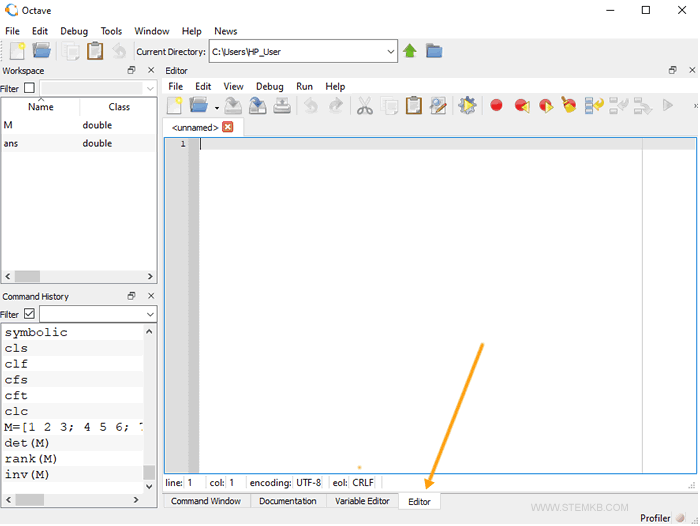
Dans la barre en bas se trouve l'élément Éditeur ( Editor ) qui vous permet d'écrire et d'enregistrer des scripts sur Octave.

Comment installer GNU Octave

Vous pouvez télécharger le fichier d'installation directement sur le site officiel www.gnu.org/software/octave/

Il est disponible pour n'importe quel système d'exploitation de PC : Linux, Windows, MacOS, BSD

Si vous utilisez Linux, vous pouvez également le trouver parmi les applications pouvant être installées dans les différents dépôts.

Dans ce guide, je vais expliquer quelques exemples pratiques d'utilisation d'Octave.

• Comment effectuer des opérations mathématiques élémentaires
  Découvrez les opérateurs mathématiques utilisés par Octave pour effectuer des opérations mathématiques de base.
  
• Comment faire l'approximation rationnelle d'un nombre réel
  Dans cette leçon, je vais expliquer comment transformer un nombre réel en une somme de fractions..
  
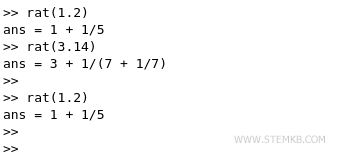
• Comment épeler pi, l'infini, l'unité imaginaire ou le nombre d'Euler?
  Octave utilise des constantes prédéfinies spécifiques pour indiquer pi, le symbole de l'infini, le nombre d'Euler et l'unité imaginaire.
  
• Comment calculer les logarithmes
  Dans cette leçon, je vais expliquer comment calculer les logarithmes naturels, les logarithmes de base 10 ou 2 à l'aide des fonctions prédéfinies d'Octave, et comment calculer les logarithmes avec n'importe quelle autre base.
  
• Comment effectuer des opérations avec des nombres complexes
  Dans ce guide, je vais expliquer comment effectuer des opérations mathématiques avec des nombres complexes.
  
• Comment calculer la limite d'une fonction
  Dans cette leçon, je vais expliquer comment calculer la limite d'une fonction pour x qui tend vers un point ou vers plus ou moins l'infini.
  
• Comment calculer la dérivée d'une fonction
  Dans ce guide, je vais expliquer comment calculer la première, deuxième ou n-ième dérivée d'une fonction.
  
• Calcul des intégrales indéfinies (antidérivées)
  Dans cette leçon, nous explorerons le processus de détermination de l'intégrale indéfinie d'une fonction.



• Comment calculer l'intégrale définie d'une fonction
  Dans cette leçon, nous apprendrons comment calculer l'intégrale définie d'une fonction entre deux limites d'intégration.
  
• Comment trouver la solution d'une équation différentielle
  Dans cette leçon, je vais expliquer comment calculer une équation différentielle homogène ou non homogène du premier ou du second ordre.
  
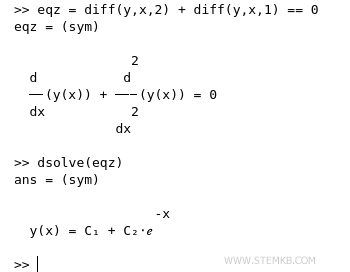
• Comment créer un vecteur
  Dans cette leçon, nous apprendrons comment définir un vecteur dans Octave et les principales opérations sur les vecteurs.
  
• Comment créer des matrices
  Dans cette leçon, je vais démontrer comment créer une matrice carrée ou rectangulaire.
  
• Résolution d'un système d'équations linéaires
  Dans cette leçon, je vous guiderai à travers le processus de résolution d'un système d'équations linéaires en utilisant le calcul vectoriel dans Matlab pour déterminer les solutions.