Comment déterminer la longueur d'un vecteur avec Octave
Dans ce cours, je vais vous montrer comment calculer la longueur d'un vecteur en utilisant Octave.
Qu'entend-on par la longueur d'un vecteur ? Il s'agit de la distance euclidienne que représente le vecteur. On l'appelle également norme. Par exemple, la norme euclidienne d'un vecteur correspond à la longueur de la flèche.
Je vais illustrer cela avec un exemple concret.
Définissons un vecteur dans la variable V
>> V=[3 4]
V =
3 4
Nous avons donc un vecteur dont le point d'arrivée est (3;4).
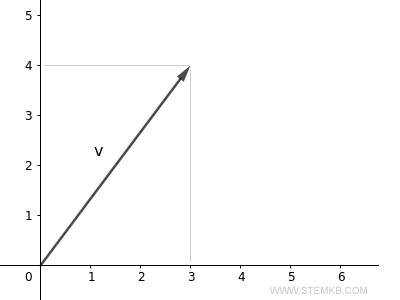
Pour obtenir la longueur du vecteur (ou sa norme), il suffit d'utiliser la fonction norm(V)
>> norm(V)
ans = 5
La longueur de notre vecteur (ou norme) est donc de 5.
C'est la longueur de la flèche dans le plan cartésien.
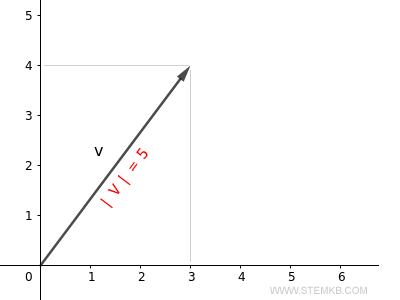
Vérifions-le. On peut calculer la longueur d'un vecteur (ou module) en utilisant le théorème de Pythagore $$ | \vec{v} | = \sqrt{3^2+4^2} = \sqrt{25} = 5 $$ La longueur du vecteur est bien de 5. Notre résultat est donc correct.