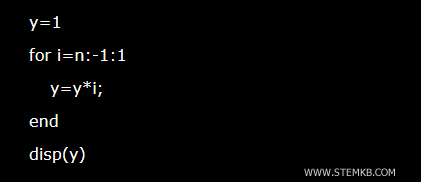Fonctions récursives dans Octave
Dans cette leçon, je vais vous expliquer comment utiliser la récursion dans les fonctions d'Octave.
La récursion se réfère à la technique d'une fonction qui s'appelle elle-même plusieurs fois. C'est un concept fondamental de la programmation fonctionnelle.
Pour vous aider à comprendre ce concept, permettez-moi de vous fournir un exemple pratique.
Vous pouvez utiliser la récursion pour calculer le factoriel d'un nombre.
1;
function y = fact(x)
if (x<0)
disp("negative number")
return;
endif
if (x<2)
y=1;
return;
else
y=x*fact(x-1)
endif
endfunction
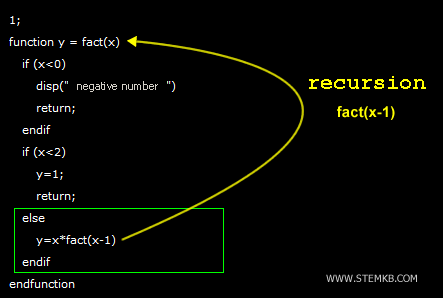
Dans ce script, j'ai défini une fonction appelée fact() qui prend une entrée numérique (x).
- Si x<0
Tout d'abord, la fonction vérifie si l'entrée est négative. Si x<0, la fonction affiche un message indiquant que le nombre est négatif et termine l'appel de fonction en utilisant l'instruction return. Cela est dû au fait que le factoriel d'un nombre négatif est indéfini.

- Si 0≤x<2
Ensuite, la fonction vérifie si l'entrée est inférieure à 2. Si 0≤x<2, la fonction retourne 1 et termine la récursion. L'instruction return renvoie la valeur 1 à l'appel de fonction précédent, fermant ainsi la boucle récursive.

- Si x≥2
Enfin, si l'entrée est supérieure ou égale à 2, la fonction multiplie le nombre d'entrée x par le résultat de fact(x-1). Cela est réalisé grâce à la récursion, où la fonction s'appelle elle-même avec une nouvelle entrée de x-1, qui est le nombre entier actuel x réduit de un. Le processus se répète jusqu'à ce que le cas de base de x<2 soit atteint et que la récursion se termine.tes.
En somme, cette fonction offre une façon efficace de calculer le factoriel de nombres entiers non négatifs.
Par exemple, vous pouvez appeler la fonction fact() que vous venez de créer et passer 6 comme paramètre initial.
La fonction prend le nombre d'entrée x=6 et calcule récursivement le factoriel.
n=6
y=fact(n);
disp(y)
Le script affiche le nombre 720, qui est le factoriel de 6!
720
Pourquoi la sortie de la fonction est-elle 720?
La fonction s'appelle elle-même cinq fois (récursion) en passant un nombre progressivement plus petit.
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)
Dans le dernier appel fact(1)=1, la fonction retourne 1 car la valeur d'entrée (x=1) est inférieure à deux.
À ce stade, la récursion se termine et le processus revient en arrière en fermant tous les appels
Si fact(1)=1 alors fact(2)=2 car fact(2)=2*fact(1)=2*1=2
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2
Si fact(2)=2 alors fact(3)=6 car fact(3)=3*fact(2)=3*2=6
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)=3*2=6
Si fact(3)=6 alors fact(4)=24 car=4*fact(3)=4*6=24
fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)=4*6=24
Si fact(4)=24 alors fact(5)=120 car fact(5)=5*fact(4)=5*24=120
fact(6)=6*fact(5)
fact(5)=5*fact(4)=5*24=120
Si fact(5)=120 alors fact(6)=720 because fact(6)=6*fact(5)=6*120=720
fact(6)=6*fact(5)=6*120=720
Ainsi, le factoriel de 6! est 720.
$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$
Note. Dans cet exemple, j'ai créé une fonction de factoriel pour expliquer comment fonctionne la récursivité dans Octave. Cependant, si vous avez seulement besoin de calculer le factoriel, n'oubliez pas qu'Octave a également une fonction prédéfinie spécifique, factorial(x), qui est beaucoup plus pratique à utiliser. De plus, vous pouvez calculer le factoriel en développant une fonction basée sur l'itération sans utiliser la récursivité, et le résultat sera toujours le même.