Le produit vectoriel sous Geogebra

Dans ce tutoriel, je vous accompagne pas à pas dans le calcul du produit vectoriel de deux vecteurs à l'aide de Geogebra.

Initiez-vous en créant deux vecteurs dans un espace tridimensionnel.

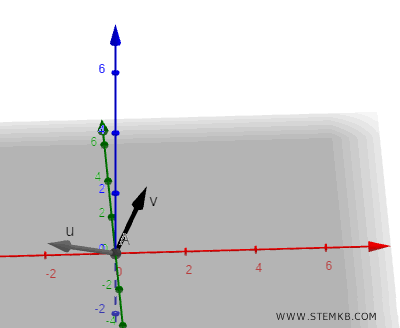
Le premier vecteur se définit par

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

Quant au second vecteur, il est défini par

$$ \vec{u} = \begin{pmatrix} -2 \\ -1 \\ 1 \end{pmatrix} $$

Si la création d'un vecteur vous est encore inconnue, je vous invite à consulter notre leçon en ligne sur comment construire des vecteurs avec Geogebra.

Par la suite, insérez ProduitVectoriel(v,u) dans le champ de commande de Geogebra et validez avec Entrée.

Les lettres u et v correspondent ici aux noms des vecteurs que vous venez de définir.

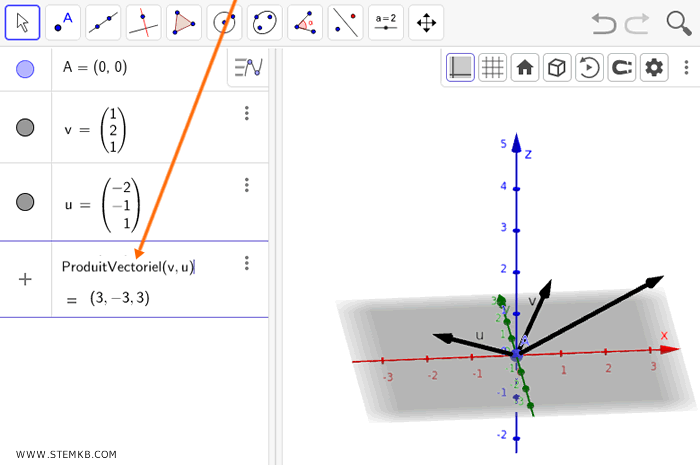
Geogebra procède alors au calcul et à l'illustration du produit vectoriel de vos vecteurs.

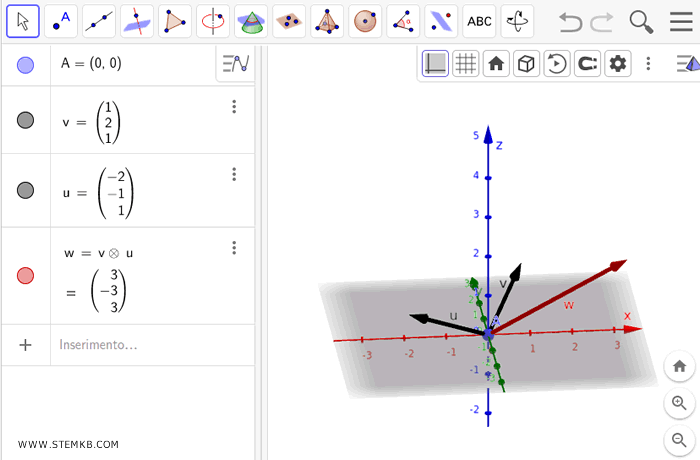
Dans cet exemple, le vecteur résultant du produit vectoriel est w, avec pour coordonnées :

$$ \vec{w} = \begin{pmatrix} 3 \\ -3 \\ 3 \end{pmatrix} $$

En quoi le produit vectoriel est-il essentiel ? Le produit vectoriel entre deux vecteurs u et v engendre un troisième vecteur w, se distinguant par sa position perpendiculaire aux deux premiers. L'orientation de ce vecteur résultant est dictée par l'ordre des vecteurs initiaux. Si ceux-ci sont parallèles, le résultat est un vecteur nul. L'ampleur du produit vectoriel traduit la superficie délimitée par les deux vecteurs sur leur plan commun.

Si vous avez apprécié ce guide pratique de StemKB, ne manquez pas nos prochaines publications.