Calcul du rang d'une matrice avec Geogebra

Dans ce tutoriel, vous allez découvrir comment déterminer le rang d'une matrice carrée à l'aide de Geogebra.

Qu'est-ce que le rang d'une matrice ? C'est le niveau le plus élevé parmi les sous-matrices carrées de la matrice qui possèdent un déterminant différent de zéro.

Commencez par saisir une matrice carrée.

Prenez, par exemple, une matrice de dimension 3x3 avec trois lignes et trois colonnes.

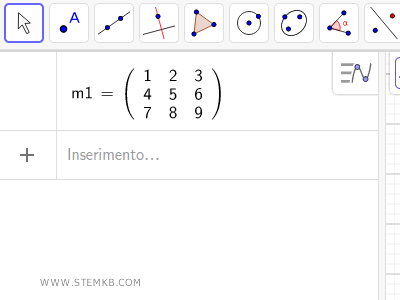
Remarque : Si la création d'une matrice sur Geogebra vous est encore inconnue, je vous recommande de consulter notre leçon précédente sur ce sujet.

Appliquez ensuite la fonction Rang() pour évaluer le rang de votre matrice.

Indiquez le nom de la matrice initiale entre parenthèses.

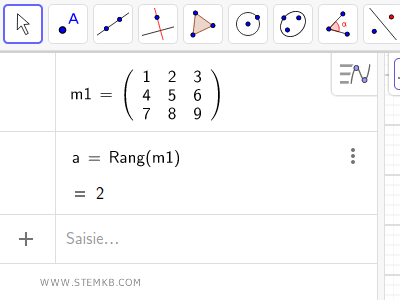
Geogebra procède au calcul et expose le rang de la matrice.

Explication. Dans cet exemple, le rang de la matrice est 2 car le déterminant de la matrice 3x3 est nul Δ (m1) = 0, ce qui exclut le rang 3.

Au moins une des sous-matrices 2x2 présente un déterminant non nul, comme le montre l'exemple de la sous-matrice en bleu avec un déterminant Δ = -2.

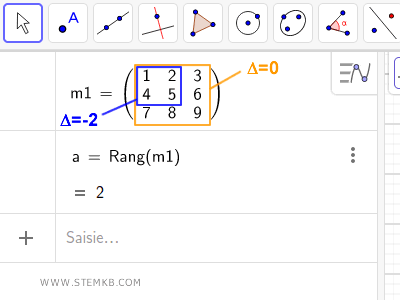
Cette sous-matrice bleue est d'ordre 2, ayant deux lignes et deux colonnes. Ainsi, le niveau le plus élevé parmi les sous-matrices avec un déterminant non nul est de deux. Les autres sous-matrices possibles auraient un ordre égal ou inférieur à celui trouvé.

Si vous avez trouvé cette explication utile, continuez de suivre nos tutoriels pour plus d'astuces et de conseils.