Calcul de la matrice inverse avec Geogebra
Dans cette leçon, nous allons explorer comment déterminer la matrice inverse à l'aide de Geogebra.
Qu'est-ce qu'une matrice inverse ? Une matrice A est considérée comme inversible lorsqu'il existe une matrice B, dite inverse, qui, multipliée par A, produit la matrice identité.
Commencez par créer une matrice carrée inversible.
À titre d'exemple, constituons une matrice 3x3 avec trois lignes et trois colonnes.
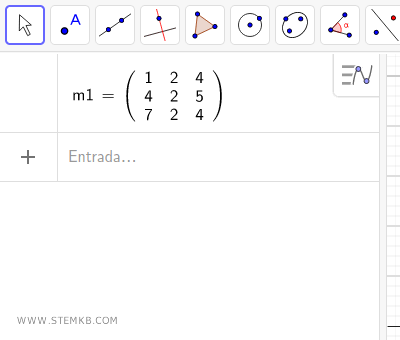
Remarque : Si vous ne maîtrisez pas encore cette étape, je vous invite à consulter notre leçon précédente sur la création d'une matrice dans Geogebra.
Ensuite, saisissez la fonction Inverser() dans un nouveau champ de saisie Geogebra.
Entrez le nom de la matrice que vous avez précédemment établie entre les parenthèses.
Geogebra procède alors au calcul et affiche la matrice inverse.
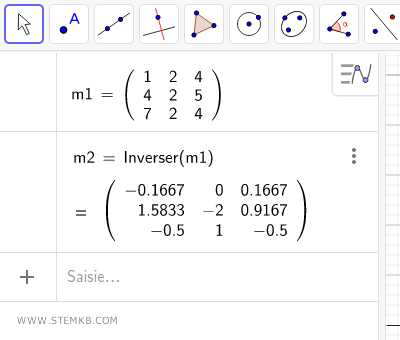
La matrice inverse est à présent calculée.
Pour confirmer le résultat, il suffit de multiplier la matrice initiale (inversible) par sa matrice inverse.
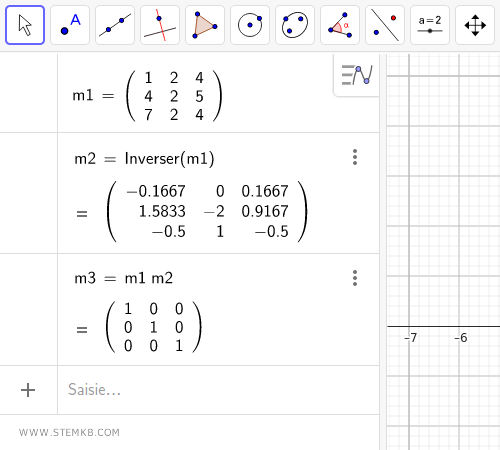
Le produit de ces matrices nous donne la matrice identité, caractérisée par des 1 sur sa diagonale principale et des zéros partout ailleurs.
Si vous trouvez cette leçon de stemKB utile, n'hésitez pas à continuer de nous suivre pour d'autres tutoriels.