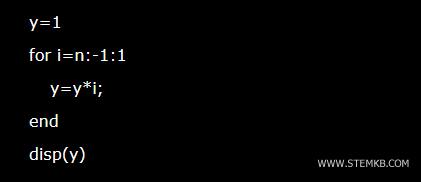Les fonctions récursives dans Matlab

Approfondissons aujourd'hui la notion de fonctions récursives dans Matlab, un sujet à la fois riche et fascinant.

Qu'est-ce que la récursivité ? En programmation, une fonction récursive est celle qui fait appel à elle-même dans son exécution. Ce concept, pierre angulaire de la programmation fonctionnelle, se révèle particulièrement pertinent pour résoudre des problématiques spécifiques.

Laissez-moi vous en donner un exemple concret.

Imaginez que vous devez calculer la factorielle d'un nombre (n!). Pour cela, vous pourriez écrire une fonction récursive de cette manière :

function y = fact(x)
if (x<0)
disp("nombre négatif")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1);
end
end

Cette fonction, nommée fact(), incarne la récursivité par son appel à elle-même dans l'expression y = x * fact(x - 1).

Examinons maintenant son fonctionnement.

Au départ, la fonction fact() reçoit un paramètre x. Suivons son processus :

• Si x<0
  Un x négatif ne permet pas de calculer une factorielle. Dans ce cas, la fonction signale l'erreur par "nombre négatif" et interrompt son exécution avec return.
  
• Si 0≤x<2
  Pour un x positif mais inférieur à 2, la fonction retourne simplement 1, mettant fin à la récursivité sans nouvel appel à elle-même.
  
• Si x≥2
  Pour un x supérieur ou égal à 2, fact() se calcule en multipliant x par le résultat de fact(x - 1), s'appelant ainsi de façon récursive.
  

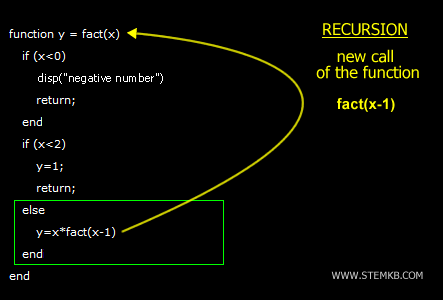
Prenons l'exemple de fact() appelée avec x = 6.

n=6;
y=fact(n);
disp(y)

function y = fact(x)
if (x<0)
disp("nombre négatif")
return;
end
if (x<2)
y=1;
return;
else
y=x*fact(x-1);
end
end

Remarque. Il est important de rappeler qu'en Matlab, une fonction doit toujours être définie à la fin du script.

En recevant x = 6, la fonction entreprend le calcul de 6! de manière récursive.

Elle s'auto-invoque cinq fois, décrémentant à chaque étape la valeur de x.

fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)

Lors du dernier appel, fact(1) = 1, la fonction renvoie 1, finalisant ainsi les appels récursifs précédents.

Si fact(1) = 1, alors fact(2) s'évalue à 2, car fact(2) = 2 * fact(1) = 2 * 1 = 2, et ainsi de suite.

fact(6)=6*fact(5)
fact(5)=5*fact(4)
fact(4)=4*fact(3)
fact(3)=3*fact(2)
fact(2)=2*fact(1)=2*1=2

En suivant cette logique, on détermine que la factorielle de 6 est 720.

$$ 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 $$

En conclusion, la factorielle de 6 s'établit à 720.

720

Note. Dans cet exemple, nous avons créé une fonction récursive pour calculer la factorielle d'un nombre. C'est un exemple éloquent pour illustrer le principe de la récursivité. Néanmoins, Matlab propose aussi la fonction prédéfinie factorial(x) pour calculer la factorielle sans nécessiter une nouvelle fonction.

factorial(6)=720

Il est également possible de calculer la factorielle d'un nombre en utilisant une fonction itérative, sans recourir à la récursivité. Le résultat final reste identique.

Voici un algorithme exemple pour le calcul de la factorielle par itération :