Calcul intégral avec GeoGebra

Dans notre tutoriel du jour, plongeons ensemble dans la méthode de calcul de l'intégrale indéfinie d'une fonction grâce à GeoGebra, le tout illustré par un exemple concret.

Abordons les fondamentaux : qu'est-ce qu'une intégrale indéfinie ? Intégrer une fonction, comme f(x), consiste essentiellement à identifier une autre fonction, g(x)+k, $$ \int f(x) = g(x) + k $$ dont la dérivée D[g(x)+k] nous reconduit à notre fonction initiale f(x). $$ D_t[ g(x) + k ] = f(x) $$

Commencez par introduire une fonction dans GeoGebra. Pour notre exemple, nous sélectionnerons la fonction f(x)=x².

Continuez ensuite avec la commande Intégrale().

Entre les parenthèses de la commande, indiquez la fonction à intégrer, que nous avons appelée "f" pour cet exemple.

GeoGebra procèdera alors au calcul et exposera l'intégrale indéfinie sous la forme g(x)=1/3·x³ pour la fonction f(x) sélectionnée.

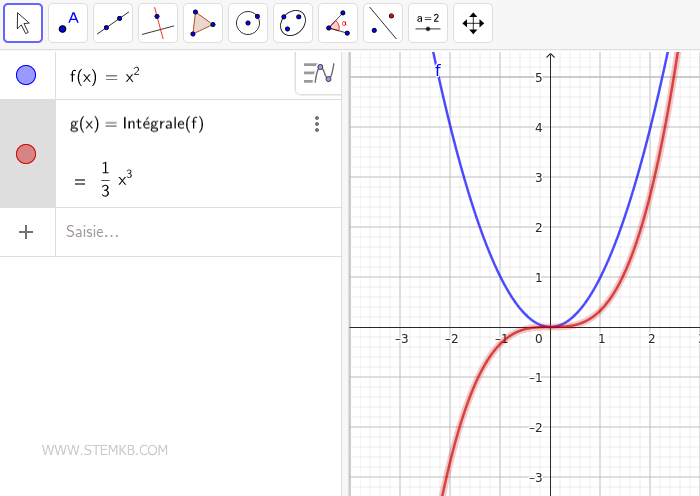
Il est essentiel de saisir que le résultat d'une intégrale indéfinie ne se limite pas à une fonction unique g(x), mais s'étend plutôt à une famille de fonctions, g(x)+k, k représentant une constante arbitraire. Cela implique qu'une expression plus précise serait g(x)=1/3·x³+k. Cette notion repose sur le fait que la dérivée de n'importe quelle constante k est toujours nulle, D[k] = 0. Par conséquent, des dérivées telles que D[1/3·x³+2] ou D[1/3·x³+3] renverront invariablement à la fonction originelle f(x)=x².

Vous souhaitez vérifier ?

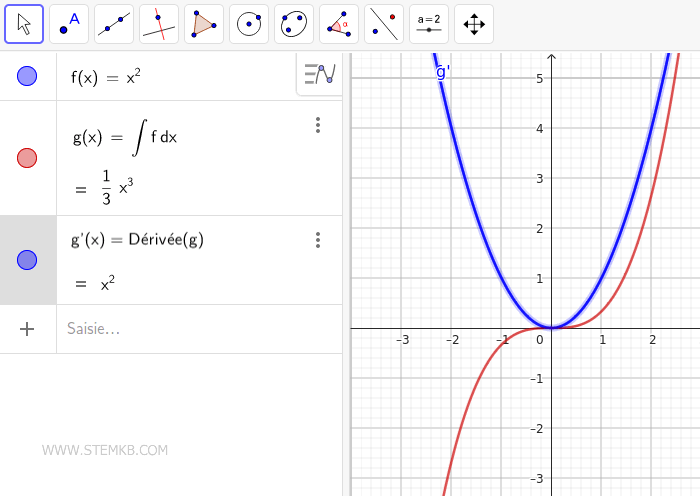
Validez vos résultats en calculant la dérivée à l'aide de la commande Dérivée().

Pour g(x)=1/3·x³, calculer la première dérivée nous renvoie effectivement à notre fonction de base f(x)=x², confirmant ainsi que la différentiation est l'opération inverse de l'intégration.

Ce guide vous a été utile ? Nous vous invitons à découvrir nos prochains tutoriels pour approfondir vos connaissances.